Механические колебания

Рис. 6

Рис.4 Рис.5

В момент t₁ соответствующий точ­ке В, нагрузка была снята. ВС соответствует быстрой деформации сокращения, CD — обратной ползучести. В результате даже за длительный период образец кости не восстанавливает своих прежних размеров, сохраняется некоторая остаточная деформа­ция .

Этой зависимости приближенно соответствует модель (рис.6, а), сочетающая последовательное соединение пружины с моделью Кельвина—Фойхта. Временная зависимость относитель­ной деформации показана на рис.6, б. При действии постоян­ной нагрузки мгновенно растягивается пружина 1 (участок ОА), затем вытягивается поршень (ползучесть АВ), после прекращения нагрузки происходит быстрое сжатие пружины 1 (ВС), а пружи­на 2 втягивает поршень в прежнее положение (ползучесть CD). В предложенной модели не предусматривается остаточная дефор­мация.

Схематично можно заключить, что минеральное содержимое кости обеспечивает быструю деформацию, а полимерная часть (коллаген) определяет ползучесть.

Если в кости или в ее механической модели быстро создать постоянную деформацию, то скачкообразно возникает и напряже­ние (участок ОА на рис.6, в). На модели это означает растяжение пру­жины 1 и возникновение в ней напря­жения. Затем (участок АВ) эта пру­жина будет сокращаться, вытягивая поршень и растягивая пружину 2, на­пряжение в системе будет убывать (релаксация напражения). Однако да­же спустя значительное время сохра­нится остаточное напряжение ст_ост. Для модели это означает, что не воз­никнет при постоянной деформации такой ситуации, чтобы пружины вер­нулись в недеформированное состоя­ние.

Ткань кровеносных сосудов (сосудистая ткань). Механиче­ские свойства кровеносных сосудов определяются главным образом свойствами коллагена, эластина и гладких мышечных волокон. Со­держание этих составляющих сосудистой ткани изменяется по хо­ду кровеносной системы: отношение эластина к коллагену в общей сонной артерии 2:1, а в бедренной артерии 1: 2. С удалением от сердца увеличивается доля гладких мышечных волокон, в артериолах они уже являются основной составляющей сосудистой ткани.

При детальном исследовании механических свойств сосудис­той ткани различают, каким образом вырезан из сосуда образец (вдоль или поперек сосуда). Можно, однако, рассматривать де­формацию сосуда в целом как результат действия давления из­нутри на упругий цилиндр.

Рис.7

Рассмотрим цилиндрическую часть кровеносного сосуда дли­ной I, толщиной h и радиусом внутренней части г. Сечения вдоль и поперек оси цилиндра показаны на рис. 7, а, б. Две половины цилиндрического сосуда взаимодействуют между собой по сечени­ям стенок цилиндра (заштрихованные области на рис.7, а). Общая площадь этого «сечения взаимодействия» равна 2М. Если в сосудистой стенке существует механическое напряжение и, то си­ла взаимодействия двух половинок сосуда равна

(1)

Эта сила уравновешивается силами давления на цилиндр изнутри (они показаны стрелками на рис.7, б). Силы направлены под разными углами к горизонтальной плоскости (на рисунке). Для того чтобы найти их равнодействующую, следует просуммировать горизонтальные проекции. Однако проще найти равнодействую­щую силу, если умножить давление на проекцию площади полу­цилиндра на вертикальную плоскость ОО'. Эта проекция равна . Тогда выражение для силы через давление имеет вид

F=p 2rl. (2)

Приравнивая (1) и (2), получаем , откуда

(3)

Это уравнение Ламе.

Будем считать, что при растяжении сосуда объем его стенки не изменяется (площадь стенки возрастает, а толщина убывает), т. е. не изменяется площадь сечения стенки сосуда (рис.7, б):

т.е. (4)

С учетом (4) преобразуем (3):

. (5)

Из (5) видно, что в капиллярах напряжение отсутст­вует .

В заключение отметим разделы и направления медицины, для которых особо важно иметь представление о пассивных механических свойствах биологических тканей:

— в космической медицине, так как человек находится в новых, экстремальных, условиях обитания;

— в спортивной медицине результативность достижений и ее
возрастание побуждают спортивных медиков обращать внимание на
физические возможности опорно-двигательного аппарата человека;

— механические свойства тканей необходимо учитывать гигиенистам при защите человека от действия вибраций;

— в протезировании при замене естественных органов и тканей искусственными также важно знать механические свойства и параметры биологических объектов;

— в судебной медицине следует знать устойчивость биологических структур по отношению к различным деформациям;

— в травматологии и ортопедии вопросы механического воздействия на организм являются определяющими.

Механическая работа человека. Эргометрия

Механическая работа, которую способен совершить человек в течение дня, зависит от многих факторов, поэтому трудно указать какую-либо предельную величину. Это замечание относится и к мощности. Так, при кратковременных усилиях человек может развивать мощность порядка нескольких киловатт. Если спортс­мен массой 70 кг подпрыгивает с места так, что его центр масс поднимается на 1 м по отношению к нормальной стойке, а фа­за отталкивания длится 0,2 с, то он развивает мощность околс 3,5 кВт.

При ходьбе человек совершает работу, так как при этом энергия затрачивается на периодическое небольшое поднятие тела и на ускорение и замедление конечностей, главным образом ног.

Человек массой 75 кг при ходьбе со скоростью 5 км/ч развивает мощность около 60 Вт. С возрастанием скорости эта мощность быстро увеличивается, достигая 200 Вт при скорости 7 км/ч При езде на велосипеде положение центра масс человека изменяется гораздо меньше, чем при ходьбе, а ускорение ног тоже меньше. Поэтому мощность, затрачиваемая при езде на велосипеде, значительно меньше: 30 Вт при скорости 9 км/ч, 120 Вт пр: 18 км/ч.

Работа обращается в нуль, если перемещения нет. Поэтому когда груз находится на опоре или подставке или подвешен на нити, сила тяжести не совершает работы. Однако каждому из нас знакома усталость мышц руки и плеча, если держать неподвижно на вытянутой руке гирю или ган­тель. Точно так же устают мышцы спины и поясничной области, если сидящему человеку поместить на спину груз. В обоих случаях груз неподвижен и работы нет. Уста­лость же свидетельствует о том, что мышцы совершают работу. Та­кую работу называют статиче­ской работой мышц.

Статики (неподвижности) такой, как ее понимают в механике, на самом деле нет. Происходят очень мелкие и частые, незамет­ные глазу сокращения и расслабления, и при этом совершается работа против сил тяжести. Таким образом, статическая работа человека на самом деле является обычной динамической работой. Для измерения работы человека применяют приборы, назы­ваемые эргометрами. Соответствующий раздел измерительной техники называется эргометрией.

Некоторые особенности поведения человека при перегрузках и невесомости

В обычных условиях на человека действуют сила тяжести и си­ла реакции опоры. При отсутствии ускорения эти силы равны и противоположно направлены. Такое состояние естественно для человека.

При ускоренном движении системы могут возникнуть особые состояния, называемые перегрузками и невесомостью.

Рассмотрим пример.

Пусть человек находится в кабине лифта (в ракете), который поднимается вверх с ускорением а. На человека дейст­вуют сила тяжести mg и сила реакции опоры F. По второму зако­ну Ньютона, F_р + mg = та, или в скалярной форме с учетом на-

правления сил

F_р - mg = та; F_p=m(g+a).

В этом случае сила реакции опоры больше силы тяжести (F > > mg), и возникают перегрузки. Так, если а = g, то F = 2mg (дву­кратная перегрузка), если а = 2g, то F_p = 3mg (трехкратная пере-

грузка) и т. д. Перегрузка выражается отношением .

Перегрузки могут оказывать существенное влияние на орга­низм человека, так как в этих состояниях происходит отток кро­ви, изменяется взаимное давление внутренних органов друг на друга, возникает их деформация и т. п. Поэтому человек способен выдерживать лишь ограниченные перегрузки.

Вестибулярный аппарат

как инерциальная система ориентации

В обычных условиях положение свободно подвешенного маят­ника указывает направление силы тяжести (рис. 4.8, а). Если ма­ятник покоится относительно ускоренно движущейся системы от­счета (неинерциальная система отсчета), то его положение зави­сит от ускорения системы а. По второму закону Ньютона,

F_н + mg = F_р = та, где результирующая сила равна по величине

F_p = mg tg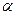, или та = mg tg 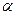, откуда

а = g tg .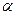

Следовательно, даже простой математический маятник в прин­ципе может быть использован для определения модуля и направ­ления ускорения системы.

Более удобным индикатором ускорения системы является уст­ройство, изображенное на рис.8. — тело известной массы ук­реплено на шести пружинках. По деформации пружин можно определить значение и направление

Рис. 8

силы, действующей на тело, а отсюда и ускорение системы, если учесть ускорение свободного падения. Такого рода индикаторы используются в инерциальной навигации, получившей развитие в связи с решением космиче­ских задач.

В самом деле, если известно ускорение системы, например ра­кеты, в каждый момент времени, то можно найти зависимость скорости от времени:

Определив v = f(t), можно найти положение системы в любой момент:

Таким образом, можно без помощи средств, находящихся вне ракеты, автономно установить ее местоположение, скорость и ус­корение в любой момент времени.

Соответствующие устройства называются инерциальными системами ориентации.

В человеческом организме имеется орган, который тоже, по су­ществу, является инерциальной системой ориентации, — это вес­тибулярный аппарат¹. Он расположен во внутреннем ухе и состо­ит из трех взаимно перпендикулярных полукружных каналов К и полости — преддверия В (рис.9). На внутренней поверхнос­ти стенок преддверия и в части полукружных каналов находят­ся группы чувствительных нервных клеток, имеющих свободные окончания в форме волосков. Внутри преддверия и полукружных каналов есть студенистая масса (эндолимфа), содержащая мелкие кристаллы фосфорнокислого и угле­
кислого кальция (отолиты). Уско­ренное перемещение головы вызыва­ет перемещение эндолимфы и отоли­тов, что воспринимается нервными клетками (через волоски). Вестибу­лярный аппарат, как и любая дру­гая физическая система, не отличает гравитационное воздействие от воз­действий, возникающих при ускоренном движении системы..

Рис.9

От системы, изображенной на рис. 4.9, вестибулярный аппарат принципиально отличается тем, что не способен количественно опреде­лить ускорение человека. Это обстоятельство не позволяет человеку, еду­щему в закрытой кабине машины, определить местонахождение автомо­биля..

Наш организм приспособился к действию силы тяжести; соответствующую привычную информацию клетки вестибулярного аппарата сообщают в мозг, поэтому состояния невесомости и перегрузок воспринимаются нами посредством вестибулярного аппарата (и других органов) как необычные состояния, к которым необходимо приспособиться.

Если оказывается периодическое воздействие на вестибуляр­ный аппарат человека, например, при качке корабля, то это мо-сет привести организм в особое состояние, называемое морской болезнью.

Дата добавления: 2013-12-13