Статистический момент сечения

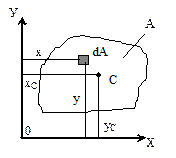Статистическим моментом сечения относительно оси, (лежащей в плоскости сечения), называется взятая по всей площади А сечения сумма произведений площадей элементарных площадок dA на их расстояние до этой оси.

Статистический момент обозначается «S» с индексом, указывающим ось.

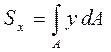
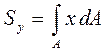
Если сечение состоит из простейших геометрических фигур (круга, квадрата, треугольника, прямоугольника), то при вычислении его статистических моментов от интегрирования можно перейти к конечному суммированию:

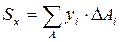
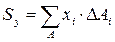
где ∆A_i – площади простейших элементов, из которых составлено сечение;

х_i и y_i – координаты центров тяжести простейших элементов.

— статический момент всей фигуры равен сумме статических моментов каждой ее части.

Вспомним теорему Вариньона: «Момент равнодействующей равен сумме (Σ) моментов её составляющих». Под знаком Σ стоят статистические моменты простейших частей сечения. Заменив эти суммы моментом всей площади относительно тех же осей, получим:

S_x = y_c · А S_y = x_c · A

где А – площадь всего сечения; x_c и y_c – координаты центра тяжести сечения.

Статистические моменты измеряются в м³. В расчётах чаще используют см³. (1 см³ = 10 ^-6 м³)

Площадь А всегда больше нуля, координаты центра тяжести сечения могут быть >0 или <0, в зависимости от расположения осей. следовательно, S_x может быть >0 или <0 в зависимости от того, где лежит большая часть площади, но может быть =0.

Если ось проходит через центр тяжести сечения, она носит название центральной оси. Статистический момент сечения относительно центральной оси =0, т.к. х_с или у_с =0.

Если сечение имеет две оси симметрии, то центр тяжести лежит на их пересечении. Если сечение имеет одну ось симметрии, то центр тяжести лежит где-то на этой оси, поэтому статистический момент симметричного сечения относительно его оси симметрии всегда =0.

При вычислении статистического момента сложного сечения его разбивают на простые части и алгебраически суммируют статические моменты этих простых частей сечения:

S_x = S_1x + S_2x + S_3x + …..+ S_nx

где S_x – статистический момент всей фигуры относительно оси x.

S_1x, S_2x, S_3x, …., S_nx – статистические моменты отдельных простых частей фигуры относительно оси x.

Статические моменты можно складывать только относительно одной и той же оси. Относительно разных осей их складывать нельзя. Для этого надо привести все моменты к единой оси и только потом суммировать.

Координаты центра тяжести сложных сечений:

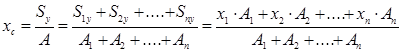
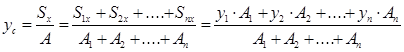
где А₁, А₂, А_n – площади простых частей, на которые разбито сложное сечение,

x₁ и y₁ – координаты центра тяжести первой простой фигуры, и т. д.

Если сечение имеет одну ось симметрии, то центр тяжести лежит где-то на этой оси, и для того чтобы определить его положение нужно найти только одну координату.

Дата добавления: 2013-12-13