Работа и энергия. Закон сохранения энергии

ЛЕКЦИЯ 5

Работа силы на пути :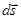

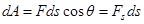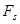, - проекция на ,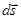

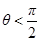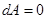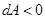при , при ,

при .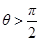

Скалярное произведение векторов и 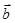: , 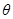- угол между векторами.

Скалярное произведение можно выразить через проекции: .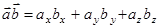

Тогда элементарную работу можно записать в виде:

.

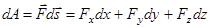Работа силы на конечном пути

Разбивая траекторию движения материальной точки на последовательность малых переме-щений 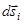, можно представить работу силы на конечном пути от точки 1 до точки 2 в виде:

или в пределе при .

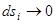
Мощность: 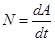(работа в единицу времени). Часто бывает удобно выражать работу через силу и скорость:

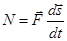или .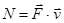

Силовое поле – совокупность всех сил, действующих на данную материальную точку в любой точке пространства.

Потенциальное силовое поле – работа сил в таком поле при перемещении материальной точки не зависит от формы пути. Примеры: гравитационное поле, электростатическое поле.

Консервативные силы – силы, действующие в потенциальном силовом поле.

Неконсервативные силы – работа зависит от формы пути (например, сила трения).

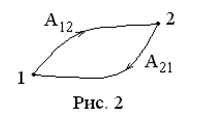
Работа консервативных сил при перемещении материаль-ной точки по замкнутому контуру равна нулю. Для консер-вативных сил 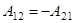(см. рис. 2), следовательно,

.

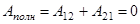Потенциальная энергия U – функция, изменение которой при перемещении материальной точки равно работе консервативной силы , взятой с обратным знаком

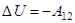. (1)

Из этого определения видно, что потенциальная энергия определена с точностью до произ-вольной константы. Например, в выражении для потенциальной энергии тела в поле тяжести вблизи поверхности Земли 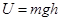по этой причине высоту можно отсчитывать от любого уровня. При вычислении работы по формуле (1) произвольная константа сокращает-ся. Для того чтобы вычислять значение самой потенциальной энергии удобно зафиксировать значение соответствующей константы. Это можно сделать по разному. Например, в электро-статике потенциал поля точечного заряда на бесконечности считается равным нулю. Можно, задать равным нулю значение 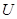в начале координат. Тогда определение потенциальной энергии можно сформулировать следующим образом.

Потенциальная энергия равна работе сил потенциального поля при перемещении материальной точки из начала координат в данную точку, взятой с обратным знаком.

Тогда

, , ,

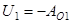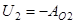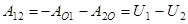, значит

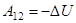. (2)

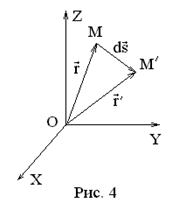
Рассмотрим бесконечно малое перемещение между двумя близкими точкам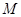и и .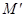

, .

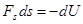Тогда 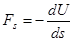. (3)

- производная по направлению (градиент).

Для проекций имеем:

, , .

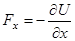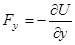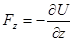В качестве примера использования этих формул вычислим потенциальную энергию материальной точки под действием упругой силы. По закону Гука 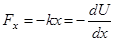. Отсюда .

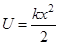Кинетическая энергия материальной точки

Рассмотрим движение материальной точки под действием произвольной силы . По второму закону Ньютона

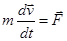. Тогда 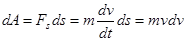или .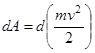

Величина называется кинетической энергией тела. Значит

,

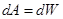то есть работа силы равна изменению кинетической энергии тела. Для консервативной силы

.

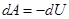Величина 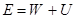называется полной энергией материальной точки. Тогда в потенци-альном поле имеет место закон сохранения энергии

или .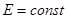

Закон сохранения энергии выполняется и для замкнутой системы материальных точек:

,

где 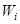- кинетическая энергия 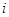-ой точки, 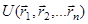- потенциальная энергия взаимо-действия материальных точек системы.

Изменение энергии под действием неконсервативных сил

Рассмотрим движение материальной точки под действием двух сил: консервативной силы и неконсервативной силы . Тогда работа суммарной силы 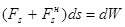. Для консервативной силы 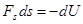. Значит 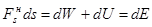. Для работы на конечном пути получим

.

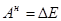Таким образом, работа неконсервативной силы равна изменению полной энергии материаль-ной точки.

Единицы измерения работы энергии и мощности

СИ: 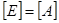= 1 Нּм = 1 Джоуль, 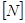= 1 Джоуль/сек = 1 Ватт.

СГС: = 1динаּсм = 1 эрг, 1 Джоуль = 10⁷ эрг, 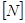= 1 эрг/сек.

Дата добавления: 2013-12-13