Лекция 7

Момент количества движения. Момент инерции твердого тела.

Мы рассмотрели два закона сохранения в механике: закон сохранения импульса и закон сохранения энергии. Каждый из законов сохранения в физике является следствием соответ-ствующего типа симметрии. Так закон сохранения импульса вытекает из однородности пространства, а закон сохранения энергии из однородности времени. Изотропность прост-ранства приводит к сохранению третьей важнейшей физической величины – момента импульса, или момента количества движения.

Момент количества движения материальной точки

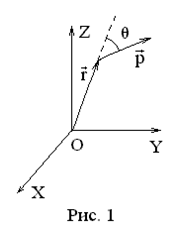
Модуль момента количества движения определяется как (см. рис. 1)

.

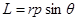Направление вектора определяется по следующему правилу. Вектор перпендику-лярен плоскости, в которой лежат вектора 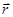и 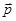. При этом, если вращать вектор 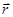по направлению к вектору 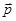, то направление совпадает с движением правого винта при таком вращении (см. рис. 2).

Такое действие над векторам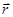и и 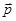в векторной алгебре называется векторным произве-дением вектора 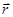на вектор 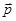и обозначается следующим образом

.

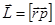Отметим, что в соответствии с таким правилом в векторном произведении важен порядок сомножителей. При перестановке сомножителей меняется знак векторного произведения

.

Для вектора момента импульса можно получить уравнение аналогичное уравнению второго закона Ньютона для импульса. Вычислим для этого производную по времени от :

.

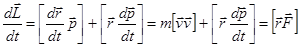Слагаемое 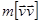равно нулю по определению векторного произведения. Последнее слага-емое в правой части называется моментом силы и обозначается

.

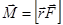Таким образом, уравнение, описывающее изменение момента импульса со временем имеет вид:

.

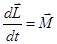Оно очень похоже на уравнение второго закона Ньютона: вместо импульса стоит момент импульса, а вместо силы – момент силы.

Для системы 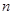материальных точек

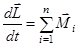, где 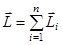- полный момент импульса системы.

Замкнутая система 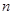материальных точек

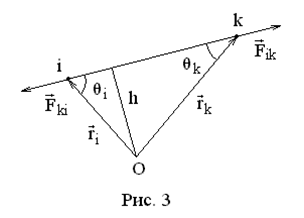Рассмотрим две точки с номерами 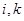. По третьему закону Ньютона 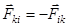. Тогда

,

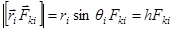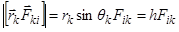и (см. рис. 3).

Величина называется плечом силы относительно т. О. Отсюда следует, что , , .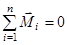

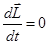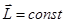Таким образом, имеет место следующий закон.

Закон сохранения момента количества движения

Полный момент количества движения замкнутой системы материальных точек остается постоянным.

Момент количества движения твердого тела, вращающегося вокруг фиксированной оси.

Мысленно разобьем твердое тело на малые элементы, которые можно считать материаль-ными точками. Момент количества движения i – го элемента

.

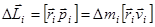Направим ось 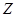вдоль оси вращения и представим вектор 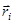в виде суммы векторов 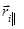и , направленных соответствен-но параллельно и перпендикулярно к оси вращения (см. рис. 4).

Тогда

.

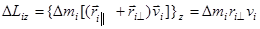Так как каждый элемент вращается по окружности с угловой скоростью 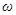, то . Следовательно, проекция полного момента импульса на ось вращения

.

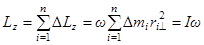Величина 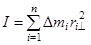при называется моментом инерции тела относительно заданной оси. Она описывает инерционные свойства вещества во вращательном движении тела. Через момент инерции выражается также кинетическая энергия вращательного движения:

или .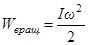

Вычисление момента инерции в общем случае сводится к вычислению объемного интеграла:

или .

Производя соответствующее интегрирование можно найти моменты инерции тел различной формы относительно заданных осей. Приведем значения моментов инерции простейших однородных тел.

1) Полый тонкостенный цилиндр с массой 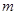и радиусом 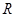. Ось совпадает с осью симметрии.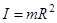

2) Сплошной цилиндр с той же осью. .

3) Сплошной шар с той же осью .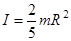

4) Тонкий стержень длины . Ось перпендикулярна стержню и проходит через его конец. .

Теорема Штейнера

Пусть момент инерции тела массы 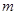относительно оси, проходящей через центр масс равен 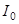. Тогда его момент инерции относительно любой оси параллельной оси, проходящей через центр масс и отстоящей от нее на расстоянии 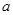равен

.

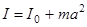Дата добавления: 2013-12-13