Эллипсоид

Исследование формы поверхностей второго порядка по их каноническим уравнениям

IV. ПОВЕРХНОСТи ВТОРОГО ПОРЯДКА

Алгебраической поверхностью второго порядка называется поверхность, уравнение которой в декартовой системе координат имеет вид:

Ax²+By²+Cz²+2Dxy+2Exz+2Fyz+gx+Hy+Iz+K= 0,

где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае получаем алгебраическую поверхность первого порядка, т.е. плоскость).

В зависимости от значений коэффициентов возможны случаи, когда уравнение определяет вырожденную поверхность (пустое множество, точку, плоскость, пару плоскостей).

Например, уравнение 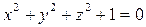не имеет решений и задает пустое множество, уравнение 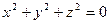задает точку с координатами (0,0,0), уравнение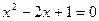задает плоскость х = 1, уравнение 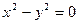задает пару плоскостей х = у и х = - у.

Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями

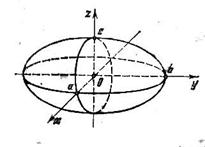
Эллипсоидом называется поверхность второго порядка с каноническим уравнением

.

Рассмотрим сечение эллипсоида плоскостью 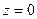. Линия пересечения эллипсоида и плоскости задается системой уравнений

Г – эллипс с полуосями а и b в плоскости .

Рассмотрим сечение эллипсоида плоскостью 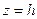. Линия пересечения задается системой уравнений

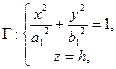
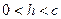где Таким образом, если , то Г – эллипс с полуосями 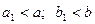в плоскост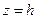и Если ,
Г – точка с координатам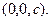и Если , система решений не имеет, т.е. исследуемая поверхность не имеет общих точек с рассматриваемой плоскостью.

Далее, так как переменная z содержится в уравнении во второй степени, плоскость 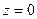является плоскостью симметрии эллипсоида. Отсюда следует, что достаточно исследовать форму поверхности и построить ее часть в области 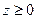, достроив затем остальную часть путем зеркального отражения найденного фрагмента поверхности относительно координатной плоскости ОXY.

Аналогично рассматриваются сечения поверхности плоскостями

Эллипсоид - замкнутая овальная поверхность, имеющая три плоскости симметрии:

Если 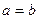, каноническое уравнение эллипсоида принимает вид 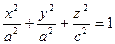. При этом линиями пересечения эллипсоида с плоскостями 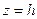, где –с < h < c, являются окружности, центры которых лежат на оси OZ и, следовательно, в этом случае эллипсоид является фигурой вращения с осью OZ.

Если 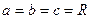, каноническое уравнение принимает вид

и задает сферу с центром в начале координат и радиусом R.

Дата добавления: 2013-12-13