Макроскопических систем

Статистический и термодинамический методы описания свойств

Лекция 1

Модуль 2. МОЛЕКУЛЯРНАЯ ФИЗИКА

В этом разделе рассматриваются системы, состоящие из огромного числа частиц (атомов, молекул), находящихся в тепловом движении. Для описания таких систем вводят следующие понятия.

Термодинамические (макроскопические) параметры - это величины, которые описывают состояние системы, не рассматривая ее внутреннее строение. К ним относят такие параметры, как температура, давление, объем и т.д.

Макросостояние системы – это такое состояние системы, которое определяется заданием ее термодинамических параметров.

Микропараметры - это координаты и скорости (импульсы) частиц системы.

Микросостояние системы – это состояние системы, определяемое заданием координат и скоростей (импульсов) всех частиц системы.

Равновесное состояние системы - такое состояние, при котором ее макропараметры принимают определенное значение и остаются постоянными сколь угодно долго.

Равновесным является такое состояние изолированной системы, в которое она переходит по истечении достаточно большого промежутка времени (в начальный момент времени состояние системы было неравновесным). Это время называют временем релаксации.

Идеальный газ – газ, частицы которого на расстоянии не взаимодействуют, а при столкновениях ведут себя как упругие шары; собственный объем частиц значительно меньше объема, занимаемого газом.

Для систем, состоящих из огромного числа частиц, находящихся в тепловом движении, наряду с механической формой движения материи появляется новая тепловая форма движения. Это можно подтвердить следующими фактами:

1) у системы появляются новые свойства (макропараметры, такие как давление, температура, электрическое сопротивление и т.д.), которыми не обладают отдельные частицы;

2) система забывает свои предыдущие состояния. Например, какое-либо равновесное состояние газа можно получить различными способами, и по конечному состоянию газа нельзя определить, какой из них был реализован. Этим тепловая форма движения материи существенно отличается от механической формы движения (в механике конечное состояние тела однозначно связано с его начальным состоянием);

3) состояние отдельной частицы не оказывает влияния на макроскопическое состояние системы. Так, например, давление газа в равновесном состоянии остается постоянным, хотя скорость какой-либо частицы из-за теплового движения постоянно изменяется.

Все это свидетельствует о том, что в этом разделе необходимо использовать другие подходы (термодинамический и статистический подходы) к описанию свойств макросистемы.

Кратко изложим суть статистического подхода, схема реализации которого приведена на рис. 2.1.

Для системы, находящейся в равновесном состоянии, из-за хаотичности теплового движения имеется большой набор случайных значений скоростей и координат частиц. Оказывается, что на огромной совокупности случайных значений скоростей, координат, кинетических энергий, потенциальных энергий отдельных частиц (первый блок на рис. 2.1) появляются строгие статистические закономерности, которые выражаются функциями распределения частиц по модулю их скоростей 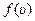, по координатам 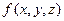, кинетическим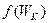, потенциальным энергиям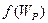и т.д. (второй блок на рис. 2.1).

Знание этих функций распределения позволяет оценить средние свойства частиц, т.е. свойства, усредненные по всей совокупности частиц (третий блок на рис. 2.1). Средние свойства частиц характеризуют всю совокупность частиц в целом. Если, например, говорят, что скорость частиц с повышением температуры возрастает, то под этим подразумевают средние скорости частиц.

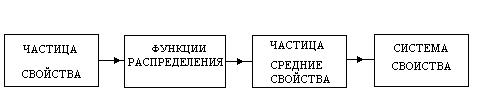
Рис. 2.1

Далее знание средних характеристик частиц позволяет получить макроскопические свойства системы (четвертый блок на рис. 2.1).

В термодинамическом подходе при описании свойств системы ее внутреннее строение не рассматривается, а все основные выводы о поведении систем делаются на основе трех начал (законов) термодинамики. Эти законы термодинамики являются постулатами (недоказуемыми утверждениями), они обобщают опытные данные. В связи с этим выводы термодинамики являются достоверными и не подвергаются сомнению.

В последующем изложении рассмотрим подробно отдельные этапы применения статистического подхода. Причем сначала будут рассматриваться системы классических частиц, т.е. частиц, для которых волновые свойства не сказываются на их движении.

Дата добавления: 2013-12-13