Общий подход

Функции распределения

Возьмем случайную величину Х, которая принимает конечный дискретный набор значений 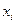(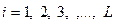). Тогда вероятностью 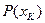выпадения в отдельном опыте какого-либо значения 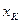этой величины называется предел отношения числа опытов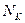, при которых выпадает это значение 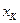, к общему числу опытов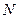, при стремлении общего числа опытов к бесконечности

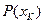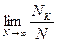=. (2.1)

При конечном числе опытов отношение (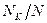) будет отличаться в ту или иную сторону от значения 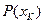, и при возрастании общего числа 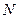опытов эти отклонения будут становиться все меньше и меньше, приближаясь к .

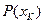Так, например, вероятность выпадения “орла” при бросании монеты равна 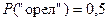. Это означает, что при бросании монеты в 50% опытов при стремлении их общего числа к бесконечности будет выпадать “орел”. При конечном числе опытов величина 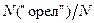будет отличаться от значения 0,5 и тем существеннее, чем меньше общее число опытов .

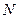Рассмотрим теперь непрерывно распределенную случайную величину Х, которая принимает непрерывный набор действительных чисел в диапазоне от нуля до бесконечности. В этом случае вероятность выпадения конкретного значения случайной величины будет равна нулю, так как число опытов (набор натуральных чисел) не перекрывает всего набора действительных чисел. Так, например, вероятность выпадения значения х = 200,00546 будет равна нулю .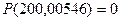

В связи с этим рассматриваются вероятности попадания случайной величины в отдельном опыте в определенный интервал значений. Для этого вводится функция распределения 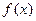, она представляет собой плотность вероятности или отношение вероятности 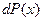попадания значения случайной величины в отдельном опыте в бесконечно малый интервал значений (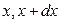) к величине этого интервала

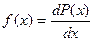. (2.2)

С помощью этой функции можно получить вероятность 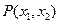попадания значения случайной величины Х в любой интервал значений (,)

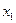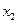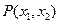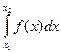=. (2.3,а)

Для малого интервала значений (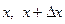), в пределах которого с достаточной степенью точности в условиях данной конкретной задачи можно считать, что функция распределения 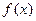не изменяется по величине, формула (2.3,а) запишется таким образом

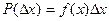. (2.3,б)

Если взять интервал значений равным области существования случайной величины (например, в пределах от нуля до бесконечности), то тогда вероятность выпадения какого-то значения случайной величины будет равна единице (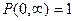), так как это будет достоверным событием

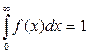. (2.4)

Выражение (2.4) получило название условия нормировки.

С помощью функции распределения 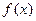можно рассчитать величины, которые характеризуют всю совокупность значений случайной величины х, такие, например, как среднее арифметическое значение 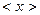, среднее квадратичное значение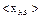

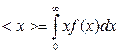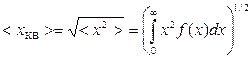, . (2.5)

Рассмотрим конкретные примеры функций распределения.

Дата добавления: 2013-12-13