График функции распределения молекул идеального газа по модулю скорости для двух температур

Для того чтобы качественно пояснить изменение графика функции распределения 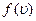при повышении температуры идеального газа, необходимо выяснить, как изменяется максимум функции 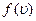. Для этого необходимо взять производную по модулю скорости от функции 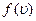и приравнять ее нулю при значении скорости 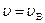. Это позволяет получить следующие формулы:

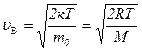, (2.12)

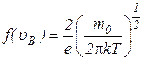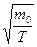~. (2.13)

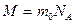В формулу (2.12) входит универсальная газовая постоянная R () и молярная масса M () газа.

Как видно из формул (2.12) и (2.13), при повышении температуры максимум функции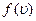становится меньше и смещается в сторону больших скоростей.

На рис. 2.3,б приведены графики функции 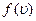для двух температур (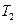>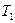). При построении графиков было также учтено, что согласно формуле (2.11) площадь под графиком функции при повышении температуры не изменяется и остается равной единице.

Как следует из графиков, приведенных на рис. 2.3,б, увеличение температуры идеального газа приводит к возрастанию числа молекул с повышенными скоростями. Так, повышение температуры приводит к возрастанию числа молекул, попадающих в приведенный на рис.2.3,б интервал скоростей (,).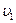

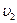Дата добавления: 2013-12-13