И равновесного состояний

Оценка термодинамической вероятности неравновесного

Покажем справедливость формулы (2.68). Для этого рассмотрим изотермическое расширение идеального газа от объема 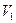до объема 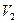. Так как процесс происходит изотермически, то это означает, что распределение молекул по скоростям не изменяется, это распределение является распределением Максвелла и определяется только температурой и массой молекул. Тогда изменения энтропии и термодинамической вероятности будут связаны с изменением распределения молекул по координатам.

Произвольная молекула при хаотичном тепловом движении независимо от других молекул может находиться в любой точке объема, занимаемого газом. Поэтому вероятность найти молекулу в любой точке пространства, занимаемого газом, будет пропорциональна объему газа, а для всех молекул – произведению этих объемов (~ 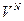,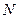- число молекул).

Возьмем натуральный логарифм отношения двух термодинамических вероятностей для конечного и начального состояний газа

,

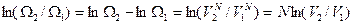где входящий в формулу коэффициент пропорциональности сокращается (он при изотермическом расширении идеального газа не изменяется).

В соответствии с формулой для изменения энтропии при изотермическом процессе (2.62б)

.

Сопоставление записанных формул для изменения энтропии и термодинамической вероятности и приводит к формуле (2.68).

Приведем доводы, поясняющие, что в состоянии равновесия наблюдается наибольший хаос в движении молекул по координатам и скоростям, т.е. ему соответствует наибольшая термодинамическая вероятность. Для этого обсудим пример расширения газа в пустоту. Сравним два состояния газа в замкнутом сосуде. В начальном состоянии газ занимает только половину объема замкнутой системы (в другой половине сосуда - вакуум, такое состояние системы при освобождении поршня будет неравновесным), а в конечном состоянии газ занимает весь объем (равновесное состояние). Учтем, что температура газа в начальном и конечном состояниях остается постоянной - (), что позволяет рассматривать при оценке 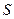и процесс перехода как равновесный изотермический процесс.

Для изотермического процесса термодинамическая вероятность будет пропорциональна объему, занимаемому системой, т.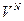е. ~ , где 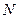- число молекул,

см. пояснение к формуле (2.72). Тогда

.

Так как для обычных систем число молекул составляет порядка 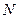~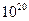, то вполне понятно, что вероятность неравновесного состояния чудовищно мала (она меньше в 2∙10²⁰ раз вероятности равновесного состояния) по сравнению с вероятностью равновесного состояния. Поэтому самопроизвольно система будет переходить в равновесное состояние, а обратный процесс, при котором все молекулы соберутся в одной половине сосуда, практически никогда в реальных условиях не реализуется.

* 2.21. Флуктуации

Согласно молекулярной физике, которая придает вероятностный характер протеканию процессов в системе, в состоянии равновесия в замкнутой системе возможно протекание процессов, при которых в разных частях ее объема энтропия может убывать, хотя в среднем для всей системы она остается постоянной. Это приводит к тому, что в разных частях системы наблюдаются отклонения термодинамических параметров системы от их средних значений, наблюдаются флуктуации этих параметров (это могут быть отклонения концентрации, температуры, давления и т.д.).

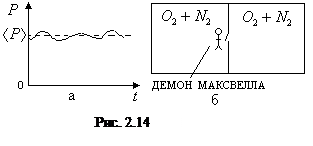
Под флуктуациями понимают отклонения термодинамических параметров системы от их средних значений на основе теплового движения молекул. Так, например, давление идеального газа в состоянии равновесия в среднем остается постоянным. Однако со временем оно будет изменяться, флуктуировать

(рис. 2.14,а). Это связано с тем, что в данный момент времени о стенку ударяется разное число молекул, что и приводит к отклонению давления от его среднего значения.

Для количественного описания флуктуаций вводится дисперсия (квадратичная флуктуация) 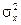, т.е. средний квадрат отклонения величины 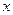от среднего значения : 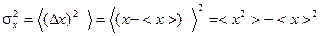, абсолютная (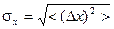) и относительная () флуктуации.

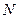При большом числе частиц системы, описывающие ее физические величины (давление, температура, концентрация молекул), практически не отклоняются от своих средних статистических значений. Это связано с тем, что относительные флуктуации 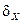будут пропорциональны 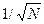. Так, например, число молекул (число Лошмидта) идеального газа в объеме 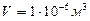при нормальных условиях равно 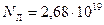, что приводит к относительной флуктуации, равной ~.

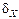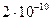Однако для малых объемов системы флуктуации могут быть достаточно большими и будут приводить к наблюдаемым эффектам. Например, голубой цвет неба связан с молекулярным рассеянием света на флуктуациях плотности воздуха. При этом интенсивность рассеянного света прямо пропорциональна четвертой степени частоты падающего излучения (закон Рэлея). Поэтому наиболее интенсивно будет рассеиваться коротковолновая часть видимого диапазона излучения (белого света), что и приводит к голубому цвету неба.

Действительно, при рассмотрении процессов рассеяния видимого света необходимо выбирать объемы, линейные размеры которых сопоставимы с длиной волны проходящего атмосферу излучения: . Такой объем воздуха содержит число молекул, равное примерно 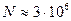, что дает для относительной флуктуации концентрации молекул значение 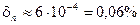. Такая относительная флуктуация является достаточно большой, что и вызывает изменение частотного состава проходящего атмосферу видимого света.

Другим примером проявления флуктуаций являются "шумы" в радиотехнических системах, под ними понимают случайные изменения (колебания) силы тока, напряжения, связанные с хаотическим движением электронов внутри металла. Частотный спектр этого шума охватывает всевозможные значения частот от нуля и выше, что приводит к уменьшению чувствительности радиоаппаратуры. При комнатной температуре интенсивность тепловых шумов остается постоянной до частот ~ .

Демон Максвелла. При развитии термодинамики в связи с ее статистическим обоснованием возникла дискуссия о возможности обойти второе начало термодинамики с помощью флуктуаций. Одним из рассматриваемых в то время примеров, позволяющих обойти второй закон термодинамики, был следующий. Внутри системы, разделенной на две части перегородкой, находилась смесь двух газов (например, азота и кислорода). Там же находился демон Максвелла - живое существо, которое могло использовать флуктуации плотности газов для его разделения (рис. 2.15,б). В перегородке было отверстие с крышкой. Когда к отверстию подлетала порция газа, в которой было больше кислорода, демон открывал отверстие и пропускал эту порцию газа, и соответственно не пропускал порцию газа, где было больше азота. Работая таким образом достаточно долго, демон мог обойти второе начало термодинамики, т.е. разделить газы в замкнутой системе.

Однако оказалось, что этого не происходит. Если бы демон был маленьким, то он сам бы испытывал флуктуации и не смог бы открыть крышку в нужное время. Если бы он был большим, то не чувствовал бы эти флуктуации. Таким образом, с помощью флуктуаций нельзя нарушить второй закон термодинамики.

* 2.22. Третье начало (закон) термодинамики

Третье начало термодинамики вытекает из формулы (2.68) для энтропии. Известно, что при температуре, равной абсолютному нулю температур (), тепловое движение отсутствует и за счет действия сил потенциального поля система занимает только одно возможное состояние - состояние с минимальной энергией. Поэтому термодинамическая вероятность будет равна единице (этому состоянию соответствует только одно микросостояние) и в соответствии с формулой (2.68) можно записать

. (2.69)

Итак, третий закон термодинамики формулируется таким образом - энтропия системы при абсолютном нуле температур равна нулю.

Существуют другие, эквивалентные, формулировки третьего закона термодинамики: 2) абсолютный ноль температур недостижим; 3) за конечное число шагов нельзя достичь абсолютного нуля температур.

Дата добавления: 2013-12-13