Термодинамика

Уравнения для явлений переноса. Линейная неравновесная

Основы физической кинетики

Лекция 6

1. Общее уравнение для явлений переноса. В классической термодинамике рассматриваются равновесные состояния и равновесные (бесконечно медленные) процессы. Для практики же представляет большой интерес изучение неравновесных процессов обмена между системой и внешними телами, протекающих с конечной скоростью.

Задача количественного описания таких процессов является довольно сложной. Наиболее разработанной является теория необратимых процессов, происходящих в открытой системе при малых ее отклонениях от положения равновесия. Этот раздел называют линейной неравновесной термодинамикой.

При малом отклонении системы от состояния равновесия можно разбить весь ее объем на малые элементы объема (они содержат макроскопическое число частиц), в пределах которых термодинамические параметры принимают вполне определенные значения (локальные термодинамические параметры). Вследствие этого для всей системы можно применять понятие термодинамических параметров, но они теперь будут зависеть от времени и координат этих элементов объема внутри системы.

К явлениям переноса относят необратимые процессы, в результате которых в системе происходит пространственный направленный перенос какой-либо физической величины (электрического заряда, массы, импульса, энергии и т.д.) на основе теплового движения частиц.

Запишем общее уравнение, которое описывает явления переноса в различных средах (газах, жидкостях и твердых телах).

Рассмотрим самый простой случай явлений переноса, когда в пространстве вдоль оси 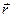создано неравномерное распределение какого-либо параметра системы (концентрация, температура, скорость движения различных слоев и т.д.).

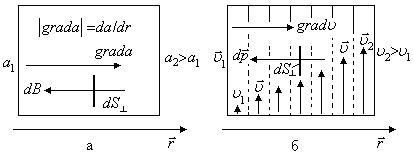
Рис. 2.15

Создадим на двух противоположных стенках системы разные значения параметра (, рис. 2.15,а), которые за счет действия внешних сил будут оставаться постоянными, тогда в пространстве возникнет стационарное распределение величины (оно со временем не изменяется).

Такое распределение можно описать вектором градиента величины , модуль которого вдоль оси 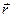будет равен (). В таких условиях в системе возникает направленный перенос (поток) другой физической величины 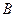, причем он будет стационарным, т.е. не будет зависеть от времени.

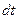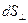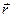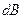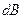За время через площадку , расположенную перпендикулярно к оси (рис. 2.15,а), будет перенесено количество величины , причем значение будет прямо пропорционально градиенту , времени переноса 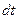и площади площадки 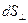, это позволяет записать следующую формулу:

. (2.70)

Формула (2.70) представляет собой общую форму записи уравнения для явлений переноса. Входящий в уравнение параметр называют коэффициентом переноса.

Физический смысл коэффициента переноса можно определить так:

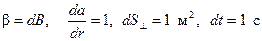, (2.71)

т.е. коэффициент переноса численно равен величине 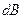, перенесенной за единицу времени через единичную площадку, расположенную перпендикулярно к направлению переноса величины 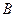, при единичном градиенте величины .

Отметим, что направление вектора градиента величины и направление переноса величины 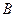будут в этом случае противоположными (рис. 12.15,а), что приводит к знаку минус в формуле (2.70).

Рассмотрим конкретные примеры явлений переноса.

2. Явление диффузии. В этом случае неравномерно распределена в пространстве плотность (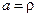) вещества (или концентрация 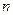), поэтому происходит перенос массы вещества ()

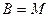. (2.72)

Это уравнение получило название уравнения диффузии, или уравнение Фика, а коэффициент 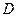называют коэффициентом диффузии.

Различают явления диффузии и явление самодиффузии. Под явлением диффузии понимают процессы выравнивания концентраций (плотности) в смеси нескольких веществ. В этом случае выравниваются концентрации для отдельных веществ в смеси по всему объему, занимаемому системой. Под явлением самодиффузии понимают процессы выравнивания концентрации (плотности) для одного вещества.

3. Явление теплопроводности. Температура противоположных стенок системы поддерживается различной (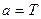), поэтому возникает перенос тепла ()

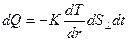. (2.73)

Уравнение (2.73) называют уравнением теплопроводности или уравнением Фурье, а коэффициент 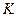называют коэффициентом теплопроводности.

4. Явление внутреннего трения (явление вязкости). В системе создается, например, направленное движение газа (жидкости) вдоль стенок сосуда

(рис. 2.15,б). Распределение скорости направленного движения по сечению будет неравномерным. Если разбить объем газа (жидкости) на отдельные слои, то их скорость будет разной - вблизи стенки она будет наименьшей, а вдали от нее наибольшей.

Молекулы каждого слоя движутся вместе с ним со скоростью направленного движения и одновременно участвуют в тепловом движении. За счет теплового движения молекулы будут переходить из одного слоя в другой, при этом происходит перенос импульса направленного движения (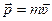), вследствие этого на границе слоев возникают силы трения, которые тормозят движение более быстрого слоя и увеличивают скорость более медленного слоя.

В явлении вязкости в пространстве неравномерно распределяется скорость направленного движения слоев газа (), вследствие чего происходит перенос импульса направленного движения ()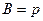

, (2.74а)

. (2.74б)

В формулах (2.74 а,б) коэффициент называют коэффициентом вязкости. Уравнение внутреннего трения или вязкости записывают, вводя в него силы внутреннего трения 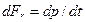, которые препятствуют движению слоев газа друг относительно друга.

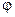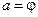5. Закон Ома в дифференциальной форме. Известно, что электроны внутри металла образуют газ свободных электронов, участвующих в тепловом движении. Для появления электрического тока (явления направленного переноса заряда) внутри металла создается внешнее электрическое поле и разность потенциалов. Тогда величина равна потенциалу (), а в пространстве происходит перенос заряда ()

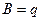. (2.75)

Эту формулу можно переписать в виде закона Ома в дифференциальной форме

,

где коэффициент 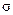называют удельной проводимостью (см. формулу (3.31)).

6. Линейная неравновесная термодинамика. Как уже отмечалось, явления переноса рассматриваются в линейной термодинамике неравновесных процессов. В ней предполагается линейная зависимость возникающих потоков 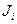от термодинамических сил 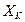, что приводит к уравнениям типа

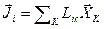, (2.76)

где 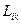- кинетические коэффициенты или коэффициенты переноса.

В прямых процессах термодинамическая сила 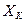вызывает поток ; например, градиент температуры вызывает поток теплоты (явление теплопроводности), градиент концентрации - поток вещества (явление диффузии), градиент скорости направленного движения - поток импульса направленного движения (явление вязкости), градиент потенциала - поток заряда (электрический ток). Такие процессы характеризуются кинетическими коэффициентами (их называют коэффициентами переноса), пропорциональными коэффициентам теплопроводности, диффузии, вязкости и удельной проводимости.

Следствием таких уравнений (2.76) является существование перекрестных процессов (), а именно, градиент температуры может вызвать поток вещества в многокомпонентных системах (явление термодиффузии, эффект Соре), а градиент концентрации - поток теплоты (диффузионный термоэффект, эффект Дюфура).

Отметим, что в нелинейной неравновесной термодинамике изучаются процессы, происходящие в системах при больших отклонениях ее от состояния равновесия. В этом случае была обнаружена возможность самоорганизации в открытых неравновесных системах, т.е. протекания таких процессов, при которых энтропия системы уменьшается. При этом происходит образование структур, которые могут играть существенную роль при развитии окружающего мира.

Дата добавления: 2013-12-13