Прямая и обратная геодезические задачи

Прямая геодезическая задача формулируется следующим образом: даны координаты некоторой начальной точки А, а также направление и расстояние от точки А к точке В. Необходимо определить координаты точки В.

При этом в геодезии всегда имеется в виду, что задано направление кратчайшей линии и минимальное расстояние между точками. В навигации в аналогичной задаче, называемой счислением пути, обычно подразумеваются заданными направление локсодромии и ее длина. Кроме того, в обеих интерпретациях, в зависимости от величины заданного расстояния S₀ и требуемой точности расчета координат φ₁ и λ₁, эта задача может решаться на эллипсоиде (с учетом сферичности Земли), на сфере или на плоскости.

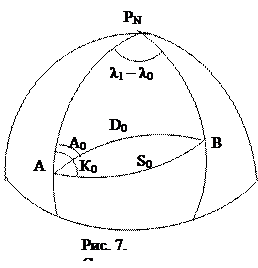При больших расстояниях между точками прямая геодезическая задача решается на эллипсоиде или сфере. В геодезии координаты пунктов и азимуты вычисляются с точностью до 0,001΄. Это возможно лишь с учетом сфероидичности Земли на основе применения численных методов интегрирования системы уравнений (2.16)÷(2.18). В судовождении, как правило, достаточная точность (до 0,1') обеспечивается использованием формул сферической тригонометрии.

Рассмотрим сферический треугольник АРВ (рис.7), образованный дугами меридианов в начальной и конечной точек, равными90⁰-φ₀ и 90⁰-φ₁, а также соединяющей длиной D₀. Сферический угол при полюсе Р_N равен разности долгот λ₁ – λ₀, а угол между северной частью меридиана начальной точки и ортодромией равен А₀ (иногда его обозначают П₀ или 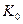). Известными являются величины φ₀, λ₀, Α₀ и D₀.

Для определения широты φ₁ можно воспользоваться теоремой косинуса стороны сферического треугольника, согласно которой

,

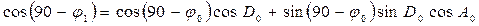откуда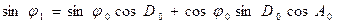

Долгота λ₁может быть найдена как с использованием уже рассчитанной широты φ₁, так и независимо от φ₁. Рассмотрим независимое решение, которое выполняется с помощью теоремы котангенсов.

,

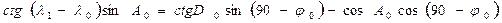откуда .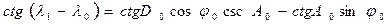

Для расчетов на калькуляторе эта формула преобразуется так, чтобы использовались только функции синуса, косинуса и тангенса:

.

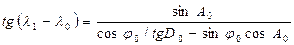В задаче счисления пути, близкой по сути к прямой геодезической задаче, заданы координаты начальной точки φ₀ и λ₀, направление пути 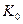и пройденное расстояние S₀. Определение координат φ₁ и λ₁ конечной (или текущей точки производится исходя из уравнений локсодромии на сфере где главные радиусы кривизны Ν1 и Ν для любой точки поверхности равны радиусу сферы R (см. уравнения (23) и (24)):

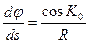; (2.24)

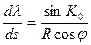. (2.25)

Интегрирование уравнения (2.24) не представляет затруднений, так как его правая часть является постоянной величиной

.

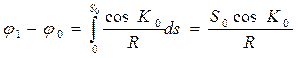Если расстояние Ѕ₀ выражено в морских милях, то разность широт по этой формуле получается в радианах. Для перехода к угловым минутам необходимо это значение разделить на arc1´, а так как R arc1´=1, то разность широт в минутах находят по формуле

.

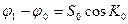Уравнение (32) содержит в правой части переменную величину φ. Интегрирование его можно выполнить по аналогии с выводом уравнения локсодромии (см. п.3.4.). В результате получается формула (2.21) с 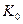вместо А и без второго слагаемого в квадратных скобках:

(2.26)

При значениях 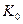близких к 90⁰ или 270⁰ этой формулой воспользоваться нельзя, т.к. tg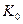-¥. Но при этом величина φ практически не изменяется. Считая φ постоянным, равным φ₀, получаем следующее решение уравнения (2.25)

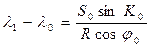
причем sin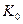= 1 при 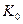= 90⁰ и sin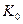= -1 при 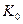= 270⁰.

Обе последние формулы дают разность долгот в радианах. Переход к угловым минутам производится делением этих значений на arc1´=1/3437,75, поэтому для практического использования эти формулы записываются в виде:

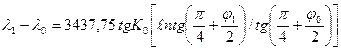(2.27)

при |K₀-90|≥1º и |K₀-270|≥1º;

λ₁ – λ₀ = S₀ / cosφ₀ при |K₀-90|<1º;

λ₁ – λ₀ = - S₀ / cosφ₀ при |K₀-270|<1º;

При малых расстояниях между начальной и конечной точками локсодромия и ортодромия практически сливаются в одну линию и рассмотренная задача в навигации обычно решается графически путем построения на карте.

Обратная геодезическая задача формулируется так: даны координаты точек А(φ₀, λ₀) и В(φ₁, λ₁); определить направление и расстоянию от А к точке В.

В большинстве случаев кратчайшее расстояние между двумя точками на поверхности Земли и направление кратчайшей линии можно рассчитать с достаточной для целей навигации точностью по формулам сферической тригонометрии. В сферическом треугольнике АР_ΝВ (см. рис.7) при этом известны дуги меридианов, равные 90º - φ₀ и 90º - φ_1, а также угол между ними, λ₁ – λ₀.

Ортодромическое расстояние D₀ находится по формуле косинуса стороны с учетом тождеств cos(90 - φ₀) =sinφ₀, sin(90 – φ₀) = cosφ₀ и т.п.:

cosD₀=sinφ₀ sinφ₁ + cosφ₀ cosφ₁ cos(λ₁ – λ₀). (2.28)

Если требуется повышенная точность определения кратчайшего расстояния между точками, то следует исправить величину D₀ поправкой за сфероидичность Земли, которую можно рассчитать по формуле Андуайе-Ламберта

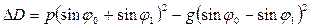, (2.29)

где ; .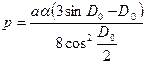

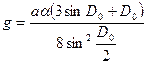В приведенной формуле величина D₀, не являющаяся аргументом тригонометрических функций, должна быть выражена в радианах. Величина ΔD получается в таких же единицах длины, в каких задана большая полуось 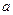земного сфероида. Если 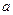- в метрах, то для представления ΔD в милях необходимо разделить результат на 1852.

Исправляемое расстояние D₀ относится к сфере с радиусом, равным 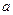. Поэтому расстояние D₀ (в милях) определяется как произведение угла D₀ (в радианах) на 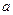(в милях). Длина геодезической линии D_Г = D₀ + ΔD.

Направление кратчайшей линии от точки А к точке В в навигационных задачах можно всегда считать совпадающим с направлением ортодромии и находить по формуле котангенсов

,

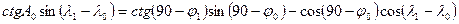откуда .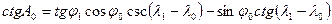

Для вычислений на калькуляторе эту формулу целесообразно представить в виде

.

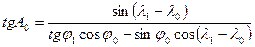В навигации существует задача расчета плавания по локсодромии, в которой по координатам двух точек требуется определить курс 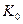и протяженность пути S₀ из одной точки в другую. Такая задача с достаточной точностью решается на основе полученных ранее уравнений локсодромии на сфере (см. формулы (2.27)¸(2.29)).

Для нахождения локсодромического курса К₀ из точки А(j₀, l₀) в точку В(j₁, l₁) рассчитывается величина

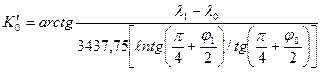, (2.30)

где разность долгот l₁ - l₀ выражается в угловых минутах.

Величина 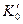находится в пределах от –90 до 90⁰. Переход от 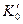к углу курса 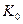производится исходя из соотношения широт и долгот начальной и конечной точек:

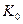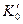= при j₁ > φ₀; λ₁ > 0;

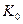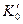= +180⁰ при j₁ < φ_0;

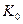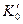= +360⁰ при j₁ > φ₀; l₁ < l₀.

Если локсодромия пересекает меридиан, соответствующий λ = 180⁰, то во всех приведенных соотношениях нужно увеличить западную долготу на 360⁰. Например, если движется в западном направлении и λ₀ = -170⁰, то нужно считать λ₀ = 190⁰; если судно движется в восточном направлении иλ₁ = -160⁰, то нужно принимать λ₁ = 200⁰.

При j₀ = φ₁ расчет по формуле (2.30) приводит к неопределенности, т.к. аргумент арктангенса стремится к бесконечности. В таких случаях локсодромический курс 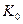с точностью до 0,5⁰ принимается равным 90⁰ при движении судна на восток (l₁ > l₀) и 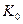= 270⁰ при движении на запад (l₁ < l₀).

Локсодромическое расстояние S₀ можно найти из уравнения (33) по известной разности широт j₁ - φ₀ и рассчитанному курсу :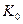

.

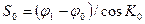Здесь j₁ - φ₀ - в угловых минутах, а S₀ – в милях.

При 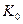близких к 90 или 270⁰ |cos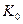| → 0 и при расчетах по формуле (35) и (36), вычислять S₀ по формуле

.

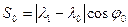На основании сравнения локсодромического и ортодромического расстояния между заданными точками делается вывод о целесообразности плавания по ортодромии и выбирается более рациональный путь судна.

Дата добавления: 2013-12-13