Элементы общей теории искажений

Основные понятия и определения

МАТЕМАТИЧЕСКАЯ КАРТОГРАФИЯ

РАЗДЕЛ 3

Вопросы для самопроверки

1. Какое значение для судовождения имеет форма и размеры земли?

2. Что такое референц-эллипсоиды и какие они бывают?

3. Какие широты точки на Земле используют в картографии?

4. Какие радиусы кривизны и длины дуг используют в судовождении?

5. Что такое геодезическая линия и какие методы её расчетов возможны?

6. Что такое локсодромия и её аналитическое описание?

7. Что такое ортодромия и соответствующие ей уравнения?

Географической картой называется уменьшенное обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону.

Одним из видов географических карт являются морские карты, которые служат для изучения района предстоящего плавания, выбора оптимального пути, планирования рейса, контроля за перемещением судна и решения других задач мореплавания. Морские карты относятся к основным юридическим документам, рассматриваемым при разборе причин навигационной аварии судов. Кроме того, морские карты используются при подготовке международных договоров по вопросам судоходства, рыболовства установления морских государственных границ и в других случаях.

Построение карты невозможно выполнить без искажения взаимного расположения объектов, находящихся на земной поверхности. Это становится совершенно очевидным, если попытаться обвернуть шар листом бумаги, не сделав ни одной складки. Однако при изображении относительно небольших участков поверхности Земли искажения становятся практически неощутимыми.

Планом называется такое изображение земной поверхности на плоскости, искажения которого не выходят за пределы точности графических построений. Точность построения линейных величин при решении задач навигации принимается равной 0,2 мм, а угловых – 0,1⁰.

Математический закон, устанавливающий соотношение между положением точек на поверхности Земли и на карте называется картографической проекцией. Уравнения и классификация картографических проекций рассмотрены в п.4.3.

Важной характеристикой карты или плана является масштаб изображения. Различают частный и главный масштабы карты.

Частным масштабом карты называется отношение длины бесконечно малого отрезка ds на карте к длине соответствующего отрезка dS на местности:

.

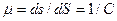Величина называется знаменателем масштаба.

Частный масштаб карты может изменяться как при переходе от одной точки к другой, так и в зависимости от направления.

Главным масштабом μ₀ называется масштаб, указанный в заголовке карты. Обычно он равен частному масштабу в какой-либо особой точке или по определенной линии и приблизительно равен среднему значению частных масштабов данной карты. На советских картах знаменатель С₀ главного масштаба выражается круглым числом, заканчивающимся не менее чем тремя нулями, например, μ₀ = 1/С₀ = 1: 100000.

В такой записи масштаб называется числовым или численным. Иногда используется линейный масштаб, который записывается, например, так: 10 км в 1 см или 5 миль в 1 см.

Масштаб плана во всех точках и по всем направлениям практически одинаков, поэтому он определяется как отношение длины любого отрезка S, взятого на плане, к длине соответствующего отрезка S на земной поверхности:

μ = s / S = 1 / С.

С увеличением района Земли, охватываемого одной картой, масштаб изображения уменьшается, а искажения в общем случае возрастают. О степени искажений в пределах одной карты можно судить по изменению частного масштаба или по тому показателю, как увеличение масштаба.

Увеличением (модулем) масштаба g называется отношение частного масштаба к главному:

g = μ / μ₀ = С₀ / С.

Для планов g=1,00. Для крупномасштабных карт (25000≤С₀≤50000) увеличение масштаба обычно в пределах 0,99<g<1,01; для путевых карт (50000<С₀≤500000) 0,90<g<1,1.; для генеральных карт (500000<С₀≤5000000) 0,70<g<1,40.

Считается, что минимальные размеры элементов какого-либо изображения, различимых невооруженным глазом, составляет порядка 0,1 мм. Практическая точность графических построения на карте редко превышают 0,2 мм. Поэтому длина линии на местности, соответствующая длине отрезка на карте или плане, равной 0,2 мм, называется предельной точностью масштаба.

Предельная точность масштаба зависит от величины масштаба карты или плана. Например, при μ=1:10000 (масштаб плана) предельная точность масштаба равна 10000*0,2 мм=2000 мм=2 м, а при μ=1:2000000 (масштаб генеральной карты) предельная точность масштаба составляет 400 м.

Качество карты определяется в значительной степени величиной и характером искажений. Эти показатели являются основными при решении вопроса о выборе картографической проекции для составления морской карты.

Для анализа искажений, присущих той или иной карте, пользуются эллипсом искажений, который получается следующим образом. В любом месте на поверхности земного сфероида можно выбрать малый круг такого радиуса r₀, в пределах которого эллипсоидальная поверхность является практически плоской. Проекция этого круга на другую плоскость всегда будет эллипсом, а проекция любой прямой, находящейся в пределах данного круга, будет также прямой в пределах полученного эллипса (рис.8).

Отношения полуосей 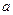и эллипса к радиусу r₀ соответствующего круга на поверхности земного сфероида равны частным масштабам карты в данных точках по данным направлениям. Причем отношение большей полуоси эллипса к кругу будет максимальным частным масштабом карты в данной точке, отношение меньшей полуоси эллипса к радиусу круга – минимальным частным масштабом.

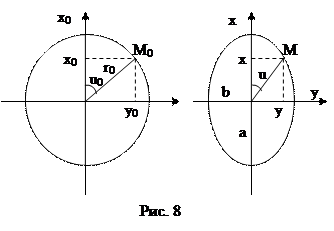
Направления, по которым частный масштаб карты достигает экстремальных значений, называется главным направлением. На всех морских картах главные направления совпадают с направлениями меридианов и параллелей. Частный масштаб вдоль меридиана принято обозначать m, а вдоль параллели – n. При таком расположении эллипса искажений, как показано на рис. 8,

m = 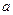/ r₀; n = b / r₀.

Определим, каковы должны быть масштабы карты по главным направлениям, чтобы углы на карте были равны соответствующим углам на местности, т.е. при каких условиях проекция будет равноугольной.

Пусть ось х на земном сфероиде и направление х большой полуоси эллипса искажений на карте совпадают с направление меридиана (см. рис.8). Выберем на окружности произвольную точку М₀ обозначим U₀, тогда

.

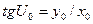На карте для соответствующей точки М

.

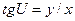Учитывая, что 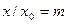и 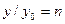, получим

; .

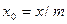Следовательно

.

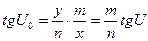Из полученного выражения видно, что проекция будет равноугольной (U=U₀) только при соблюдении равенства масштабов по главным направлениям. Таким образом, условие равноугольности проекции можно записать в виде равенства m = n.

Отсюда, в частности следует, что на карте, выполненной в равноугольной проекции, масштаб может меняться при перемещении и от одной точки к другой, но в любой точке масштаб во всех направлениях одинаков.

Дата добавления: 2013-12-13