Картографические проекции

Проекция в картографии понимается в более широком смысле, чем в геометрии. В картографии проекция рассматривается как способ переноса различных точек и линий с поверхности сфероида на плоскость. Такой перенос может осуществляться не только по нормалям к плоскости карты, как это принято в геометрии, а и по наклонным прямым, причем различные точки могут переноситься не параллельными между собой прямыми.

Уравнение картографической проекции в общем случае записывается в виде

х=ƒ₁(φ, λ); у=ƒ₂(φ, λ),

где φ, λ – географические координаты точек на земной поверхности;

х, у – картографические координаты на плоскости.

Вместо прямоугольных координат х и у часто используются полярные координаты r и q.

Функции ƒ₁(φ, λ) и ƒ₂(φ, λ) должны отвечать требованиям однозначности и непрерывности. Это значит, что каждому сочетанию j и l должна соответствовать только одна точка на карте и при непрерывном изменении j и l соответствующая точка на карте должна перемещаться также непрерывно.

С помощью уравнений (40) рассчитывается и строится картографическая сетка меридианов и параллелей, относительно которой затем наносится на карту изображение определенного участка земной поверхности. Для построения картографической сетки задаются круглыми значениями j и l, например: через 2⁰ и вычисляют соответствующие картографические координаты х и у точек пересечения меридианов и параллелей. Нанеся эти точки на бумагу, соединяют их плавными линиями и получают картографическую сетку.

Каждая карта, в зависимости от используемой при ее построении картографической проекции, обладает определенными искажениями, и имеют характерный вид изображения меридианов параллелей. Поэтому картографические проекции классифицируются по характеру искажений и по виду изображения координатной сетки.

По характеру искажений картографические проекции бывают:

1. Равноугольные (конформные) – передающие углы без искажений. В любой точке карты, построенной в этой проекции, эллипс искажений имеет равные полуоси, т. е. является окружностью. Масштаб такой карты изменяется при переходе от одной точки к другой, но в данной точке является постоянным во всех направлениях.

Морские навигационные карты строят в равноугольной проекции, масштаб которой изменяется только с широтой, оставаясь постоянным на данной параллели.

2. Равновеликие (эквивалентные) – сохраняющие постоянство масштаба площадей. Все площади на карте пропорциональны соответствующим площадям на земной сфероиде.

3. Равнопромежуточные – сохраняющие постоянство масштаба по одному из главных направлений, обычно – вдоль меридиана.

4. Производные – не обладающие свойствами равноугольности, равновеликости или равнопромежуточности, но имеющие другие существенные для решения определенных задач свойства.

По виду изображения координатной сетки картографические проекции бывают:

1. Цилиндрические, при использовании которых меридианы и параллели на карте изображаются взаимно перпендикулярными прямыми.

Уравнения цилиндрической проекции в общем случае имеют вид

х = ƒ(φ); y = 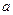λ,

где ƒ(φ) – функция, определяющая характер искажений проекции и выражающая расстояние от экватора до параллели;

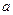- постоянная, от которой зависит расстояния между меридианами.

2. Азимутальные. На картах, построенных в азимутальной проекции, параллели изображаются концентрическими окружностями, а меридианы – радиальными прямыми, расходящимися из центра окружностей.

Картографические координаты в этом случае являются полярными координатами ρ и θ, которые находятся по формулам:

ρ = ƒ(φ); θ = λ.

В зависимости от вида функции ƒ(φ) азимутальная проекция может быть равноугольной, равновеликой или равнопромежуточной или иметь любой другой характер искажений. Например, один из видов азимутальной проекции – гномоническая – обладает важным свойством: любая дуга большого круга изображается в этой проекции прямой.

3. Конические. На картах, выполненных в таких проекциях, параллели – концентрические окружности, а меридианы – радиально расходящиеся прямые. Но, в отличие от азимутальных проекций, углы между меридианами здесь не равны разностям долгот, а лишь пропорциональны им:

ρ = ƒ(φ); θ = 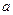λ.

Выбором функции ƒ(φ) можно задать любой необходимый характер искажений.

Конические проекции часто используются при составлении карт погоды, которые передаются на суда с помощью факсимильной аппаратуры.

Кроме перечисленных видов проекций существует еще множество других, которые относятся к произвольным, т.к. при решении задач судовождения они не используются.

Дата добавления: 2013-12-13