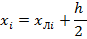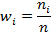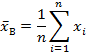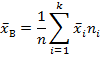Другие числовые характеристики выборки

Варианты. Вариационный ряд

Первичная обработка результатов

Небольшой объем выборки (n<25)

Пусть интересующая нас случайная величина Х принимает в выборке значение х ₁ - п ₁ раз, х ₂ – п ₂ раз, …, х_к – п_к раз, причем 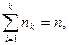где п – объем выборки.

Тогда наблюдаемые значения случайной величины х ₁, х ₂,…, х_к называют вариантами (иногда – дискретами), а п ₁, п ₂,…, п_к – частотами.

Если разделить каждую частоту на объем выборки, то получим относительные частоты: 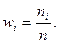Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, который может быть представлен также в виде таблицы с перечнем вариант и соответствующих им частот или относительных частот:

xi	x 1	x 2	…	xk
ni	n 1	n 2	…	nk
wi	w 1	w 2	…	wk

Пример.

При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1. Здесь n =20.

Составим вариационный ряд: 0,0,0,1,1,1,1,1,1,2,2,2,2,2,3,3,3,4,4,5.

Или в виде таблицы:

xi
ni
wi=	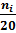0,15	0,3	0,25	0,15	0,1	0,05

Большой объем выборки (n≥25)

При большом объеме выборки вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку, то есть выборку по интервалам. Её суть состоит в том, что весь объем выборки разбивается на интервалы, рассчитывается ширина интервала (обычно она одинакова для всех интервалов), и дальнейшая обработка вариант идёт по интервалам.

1. Выбор количества интервалов k, которое зависит от числа вариант n. Два способа:

а) по формуле Стерджеса: 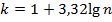; (1.1)

б) по таблице:

n	25-40	41-60	61-100	101-200	>200
k	5-6	6-8	7-10	8-10	10-15

2. Расчёт ширины h интервала:

(1.2)

3. Определение левой границы первого интервала:

(1.3)

4. Определение правой границы первого интервала, она же равна левой границе второго интервала:

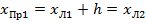. (1.4)

5. Аналогично производится расчёт границ всех интервалов:.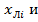

 

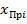6. Расчёт срединных значений интервалов, которые отстоят от левых границ интервала на величину, равную половине ширины интервалов:

(1.5)

7. Вычисление частот интервалов: подсчитывается, сколько вариант находится в каждом интервале: n₁, n₂,…n_k. Причем n₁+n₂+…+n_k=n. Этот шаг делается после ранжирования – расположения вариант по возрастанию.

8. Определение относительных частот (частостей) интервалов:

. (1.6)

Относительная частота в математической статистике играет роль вероятности, поэтому сумма относительных частот должна быть равна 1.

В случае группированной выборки получаем интервальный вариационный ряд:

xi	x1	x2	x3	…	xk
ni	n1	n2	n3	…	nk
wi=	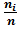w1	w2	w3		wk

1.3.2. Полигон частот. Гистограмма. Эмпирическая функция распределения

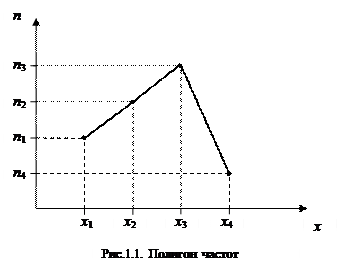Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x ₁, n ₁), (x ₂, n ₂),…, (x_k, n_k), где x_i откладываются на оси абсцисс, а n_i – на оси ординат (рис.1.1). Если на оси ординат откладывать не абсолютные (n_i), а относительные (w_i) частоты, то получим полигон относительных частот.

Заметим, что в случае интервального вариационного ряда по оси ординат откладываются срединные значения интервалов.

Другим видом графиков является гистограмма – ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат интервалы длиной h, а высотами – отрезки длиной n_i/h (гистограмма частот на рис.1.2) или w_i/h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице.

Площадь каждого прямоугольника гистограммы пропорциональна частоте (или относительной частоте) попадания случайной величины в данный интервал.

Величина n/h называется плотностью частоты.

Но вид гистограммы не изменится, если вместо плотности частоты по оси ординат отложить саму частоту (или относительную частоту).

Гистограмма по своей сути и способу построения ближе всего к дифференциальной функции распределения f(x) (закону распределения вероятностей, а точнее – плотности распределения вероятностей), широко применяющейся в теории вероятностей.

Но в теории вероятностей применяется и интегральная функция распределения случайной величины. По аналогии с ней можно задать эмпирическую функцию распределения.

Эмпирической функцией распределения называют функцию F* (x), определяющую для каждого значения х относительную частоту события X < x (события, что варианта X примет значение меньшее конкретного значения x). Таким образом,

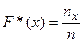, (1.7)

где п_х – число вариант, меньших х, п – объем выборки.

Замечание. В отличие от эмпирической функции распределения F* (x), найденной опытным путем, функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения. F (x) определяет вероятность события X < x, а F* (x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F* (x) стремится по вероятности к F (x).

Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F (x), а именно:

1) 0 ≤ F* (x) ≤ 1.

2) F* (x) – неубывающая функция.

3) Если х ₁ – наименьшая варианта, то F* (x) = 0 при х ≤ х ₁; если х_к – наибольшая варианта, то F* (x) = 1 при х > х_к.

При нахождении F* (x) (числителя в формуле (1.7)) для каждого интервала суммируют частоты всех предыдущих интервалов (они называются накопленными частотами):

Номер интервала				…	k
Накопленные частоты nx	n1	n1+n2	n1+n2+n3	…	n1+n2+n3+…nk=n

В итоге вид F* (x) будет подобен интегральной функции распределения для дискретной случайной величины:

Кроме рассмотренных, можно найти также следующие величины: моду; медиану; среднее арифметическое выборки (выборочное среднее)

а) для выборки малого объема:

(1.8)

б) в случае интервального вариационного ряда:

(1.9)

где 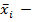среднее арифметическое каждого интервала, - частота каждого интервала, k – количество интервалов.

Дата добавления: 2013-12-13