Марковские случайные процессы

Случайный процесс

Это случайная функция от независимой переменной t (Y(t)). Реализации случайного процесса называются траекториями. Все характеристики случайных функций аналогичны характеристикам случайной функции.

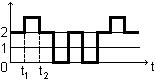Являются основным методом анализа надёжности систем: определения характеристик резервированных систем, анализ модели и контроля, поиск неисправностей и т.д. Марковский случайный процесс – это процесс, у которого в каждый момент времени вероятность любого состояния в будущем зависит только от состояния объекта в настоящий момент времени и не зависит от того, каким образом объект пришёл в это состояние. Марковский процесс – это случайный процесс без последствий. Момент времени t₁ и t₂ – моменты перехода из одного состояния в другое. Наиболее подходящим способом перехода объекта из одного состояния в другое является граф переходов.

Pij(Δt), Pji(Δt) – вероятности перехода из одного состояния в другое за некоторый промежуток времени. Важнейшая характеристика Марковского процесса. Pii(Δt) – вероятность сохранения состояния в течение некоторого промежутка времени. μ_ij, λ_ij – постоянные интенсивности прямого и обратного перехода из одного состояния за некоторый промежуток времени. Возможно представление вероятностного процесса матрицей вероятности переходов.

P₀₂=P₂₀=0

Состояние объекта в момент времени t определяется вектором

Для момента времени t+Δt вероятность состояния будет определяться

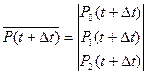
Переход объекта из состояния в момент времени t в состояние для момента времени t+Δt осуществляется преобразованием вектора в вектор с помощью транспонированной матрицы переходов .

Марковский однородный процесс – это процесс, закономерность поведения которого на любом интервале времени (t₂-t₁) не зависит от положения того интервала на оси времени. Дифференциальное уравнения можно составлять непосредственно по графу переходов по следующему правилу: в левой части каждого уравнения записывается

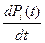, а в правой части записывается столько членов, сколько стрелок связано с этим состоянием. Каждое слагаемое равно произведению интенсивности переходов λ или μ, переводящее систему по данной стрелке на вероятность того состояния, из которого выходит стрелка. Знак перед каждым слагаемым зависит от направления перехода. Если стрелка входит в состояние, то ставится знак «+». Если выходит из состояния, то ставится знак «-». Получается система уравнений нахождения вероятностей состояний P₀(t) и P₁(t) производится с помощью преобразования Лапласа, которое позволяет перейти от дифференциальных уравнений к алгебраическим.

9. Расчёт надёжности ремонтируемой нерезервированной аппаратуры

Характеристикой надежности аппаратуры, которая учитывает сочетание свойств безотказности и ремонтопригодности и количественно оценивает готовность системы к работе, является функция готовности. К_г(t) – Функция готовности – есть вероятность застать систему в работоспособном состоянии в произвольный момент времени (t). При определении функции готовности следует учитывать, что на практике имеют место случайные процессы, т.е. процессы перехода изделия из одного состояния в другое в случайный момент времени. Такие процессы встречаются в нерезервируемой ремонтопригодной аппаратуре, резервированной неремонтируемой и ремонтируемой аппаратуре. Рассмотрим ремонтируемую нерезервированную систему.

λ – интенсивность отказов, μ – интенсивность восстановлений.

Эта система может находиться в 2-х состояниях: рабочем и отказа. Переход из рабочего состояния в состояние отказа происходит за счёт отказа системы. Для определения показателей используют граф переходов и дифференциальные уравнения.

(*)

P_i(t)→P_i(z)

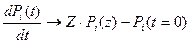
Система в нулевой момент времени должна быть работоспособной

P₀(t=0)=1; P₁(t=0)=1;

(**)

;

;

;

;

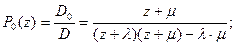
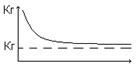
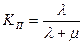
Дата добавления: 2013-12-13