Перевірка параметрів простої лінійної моделі на адекватність

Щоб мати загальне судження про якість моделі з відносних відхилень за кожним спостереженням, визначають середню помилку апроксимації:

=

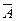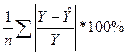
Середня помилка апроксимації не повинна перевищувати 8-10%.

Відповідно до основної ідеї факторного аналізу, загальна сума квадратів відхилень змінної Y від середнього значення 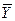розкладається на дві частини:

,

де 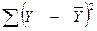– загальна сума квадратів відхилень; 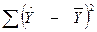– сума квадратів відхилень, пояснена регресією (або факторна сума квадратів відхилень); 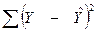– залишкова сума квадратів відхилень, що характеризує вплив неврахованих у моделі факторів.

Схема факторного аналізу має вигляд, представлений у таблиці 1 (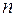 – число спостережень, 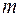– число параметрів при перемінній ).

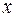Таблиця 1.

Компоненти дисперсії	Сума квадратів	Число ступенів волі	Дисперсія на один ступінь волі
Загальна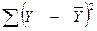
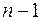
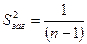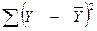
Факторна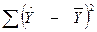
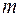
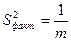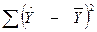
Залишкова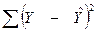

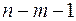
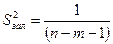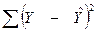
Визначення дисперсії на один ступінь свободи приводить дисперсії до порівнянного виду. Зіставляючи факторну і залишкову дисперсії в розрахунку на один ступінь свободи, одержимо величину 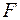-критерію Фишера:

F=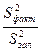= 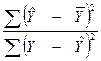(2)

Фактичне значення 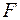-критерію Фишера (4) порівнюється з табличним значенням 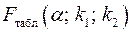при рівні значимості 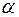і ступенях вол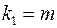і і 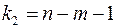. При цьому, якщо фактичне значення 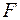-критерію більше табличного, то визнається статистична значимість рівняння в цілому.

Для парної лінійної регресії 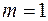, тому

F=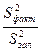= 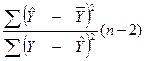(3)

У парній лінійній регресії оцінюється значимість не тільки рівняння в цілому, але й окремих його параметрів. З цією метою по кожному з параметрів визначається його стандартна помилка:.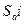

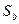Стандартні помилки коефіцієнтів регресії визначаються по формулі(1) або можуть бути розраховані слідуючим чином:

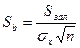, (4)

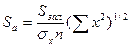, (5)

де 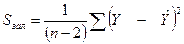– залишкова дисперсія на один ступінь свободи.

Величина стандартної помилки разом з -розподілом Стьюдента при 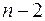ступенях волі застосовується для перевірки істотності коефіцієнтів регресії і для розрахунку його довірчого інтервалу.

Для оцінки істотності коефіцієнтів рівняння регресії його величини порівнюються з іхними стандартними помилками, тобто визначаються фактичні значення -критерію Стьюден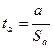та: та які потім порівнюються з табличним значенням при визначеному рівні значимості 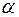і числі ступенів волі 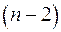. Довірчі інтервали для коефіцієнтів рівняння регресії визначаються як: 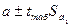i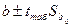

Значимість лінійного коефіцієнта кореляції перевіряється на основі величини помилки коефіцієнта кореляції S_r:

S_r=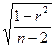. (6)

Фактичне значення -критерію Стьюдента визначається як t_r=r/m_r.

Існує зв'язок між -критерієм Стьюдента і 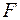-критерієм Фишера:

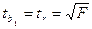. (7)

Величина 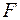-критерію зв'язана з коефіцієнтом детермінації 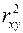, і її можна розрахувати по наступній формулі:

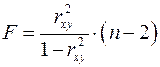
У прогнозних розрахунках по рівнянню регресії визначається 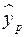значення, що розраховується, як крапковий 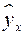прогноз 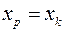при, тобто шляхом підстановки в рівняння регресії 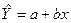відповідного значення 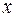. Однак крапковий прогноз явно не реальний. Тому він доповнюється розрахунком стандартної помилки 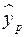, тобто 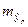, і відповідно інтервальною оцінкою прогнозного значення :

,

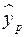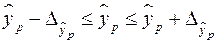де 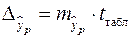, а 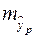– середня помилка прогнозованого індивідуального значення:

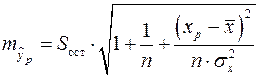. (8)

Дата добавления: 2013-12-13