Багатомірна лінійна модель регресії

Для оцінки параметрів рівняння множинної регресії застосовують метод найменших квадратів (1МНК). Для лінійних рівнянь регресії (і нелінійних рівнянь, які зводяться до лінійних) будується система нормальних рівнянь, рішення якої дозволяє одержати оцінки параметрів регресії. У випадку лінійної множинної регресії

y=a+b₁x₁+b₂x₂+…+b_mx_m
система нормальних рівнянь має вигляд:

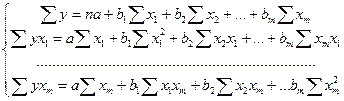
Для визначення значущості факторів і підвищення точності результату використовується рівняння множинної регресії у стандартизованому масштабі

t_y=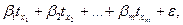

де 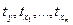- стандартизовані змінні

,

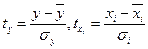для яких середнє значення дорівнює нулю, а середнє квадратичне відхилення дорівнює одиниці.

Коефіцієнти β_i звуться стандартизованими коефіцієнтами регресії.

К рівнянню множинної регресії в стандартизованому масштабі застосовують МНК. Стандартизовані коефіцієнти регресії визначаються з системи рівнянь:

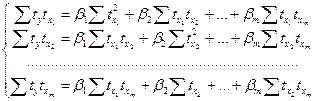
або з системи рівнянь

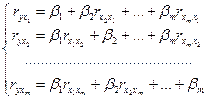
У парній залежності стандартизований коефіцієнт регресії є не що інше, як лінійний коефіцієнт кореляції r_yx.

Зв'язок коефіцієнтів множинної регресії з стандартизованими коефіцієнтами описується співвідношенням

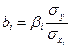
Параметр а визначається зі співвідношення

a=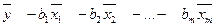

На основі лінійного множинного рівняння регресії

y=a+b₁x₁+b₂x₂+…+b_mx_m+ε

можна знайти частинні рівняння регресії, які зв’язують результативну ознаку з відповідними факторами x_i при закріплених інших, які враховуються в множинній регресії, факторів на середньому рівні. Частинні рівняння регресії мають вигляд:

……………………………………….

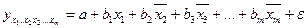
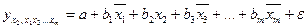
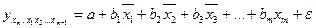
При підстановці в ці рівняння середніх значень відповідних факторів вони приймають вигляду парних рівнянь лінійної регресії, тобто маємо

…………………

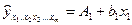
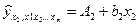
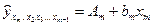
де

…………………………

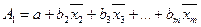
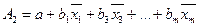
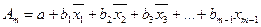
Тіснота зв’язку загального впливу всіх незалежних змінних на залежну визначається коефіцієнтами детермінації і множинної кореляції.

Щоб дати метод їх розрахунку необхідно показати, що варіація залежної змінної (Y) навколо свого вибіркового середнього значення (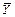)* може бути розкладена на дві складові:

1) варіацію розрахункових значень (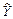) навколо середнього значення ;

2) варіацію розрахункових значень (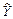) навколо фактичних (Y).

Необхідні при цьому обчислення зведемо в табл.2.

Таблиця 2

Джерело варіації	Сума квадратів відхилень	Ступені свободи	Середнє квадратів відхилень або дисперсія
Факторна ()
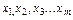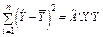
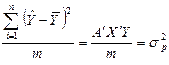
Залишок
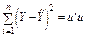
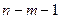
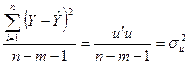
Загальна варіація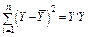

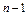
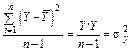
Зауважимо, що всі змінні Y i X взяті як відхилення від свого середнього значення.

Використаємо середні квадратів відхилень (дисперсії) (див. табл. 2) і запишемо формулу для обчислення коефіцієнта детермінації:

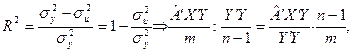(8)

або, не враховуючи ступенів свободи:

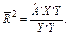(9)

Оскільки у (8) задані незміщені оцінки дисперсії з урахуванням числа ступенів свободи, то коефіцієнт детермінації може зменшуватись при введені в модель нових незалежних змінних. Тоді як для коефіцієнта детермінації, обчисленого без урахування поправки (n – 1 /m – 1) на число ступенів свободи (9), коефіцієнт детермінації ніколи не зменшується. Залежність між цими двома коефіцієнтами можна подати так:

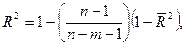(10)

де 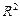— коефіцієнт детермінації з урахуванням числа ступенів свободи;

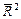— коефіцієнт детермінації без урахування числа ступенів свободи.

Для функції з двома і більше незалежними змінними коефіцієнт детермінації може набувати значень на множині 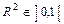. Числове значення коефіцієнта детермінації характеризує, якою мірою варіація залежної змінної (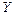) визначається варіацією незалежних змінних. Чим ближчий він до одиниці, тим більше варіація залежної змінної визначається варіацією незалежних змінних.

Множинний коефіцієнт кореляції:

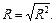
Він характеризує тісноту зв’язку усіх незалежних змінних із залежною.

Для множинного коефіцієнта кореляції з урахуваннням і без урахуванння числа ступенів свободи характерна така сама зміна числового значення, як і для коефіцієнта детермінації.

Розглянемо альтернативний спосіб обчислення коефіцієнтів детермінації і кореляції, коли система нормальних рівнянь будується на основі коефіцієнтів парної кореляції .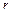

У такому разі оцінку параметрів моделі можна записати:

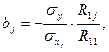(11)

де 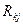— алгебраїчне доповнення матриці 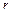до елемента .

Сума квадратів відхилень (залишків) також може бути виражена через алгебраїчне доповнення матриці :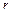

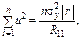
де 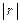— визначник кореляційної матриці. А це, у свою чергу, дає нам альтернативний вираз для коефіцієнта детермінації:

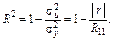(12)

Ще один альтернативний метод розрахунку коефіцієнтів детермінації на основі матриці 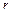можна подати у вигляді

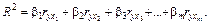(13)

Звідси коефіцієнт кореляції

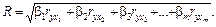(14)

Частинні коефіцієнти кореляції так само, як і парні, характеризують тісноту зв’язку між двома змінними. Але на відміну від парних частинні коефіцієнти характеризують тісноту зв’язку за умови, що інші незалежні змінні сталі.

Можна дістати спрощений вираз для розрахунку коефіцієнта частинної кореляції, обравши інший спосіб інтерпретації цього коефіцієнта. Для випадку простої регресії двох змінних маємо

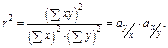
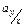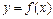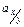де характеризує коефіцієнт при у рівнянні , а — коефіцієнт при 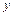в рівнянні 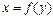. Отже, квадрат коефіцієнта парної кореляції дорівнює добутку двох наведених коефіцієнтів. Коефіцієнт частинної кореляції можна визначити аналогічно. Наприклад, розглянемо два регресійні рівняння:

;

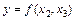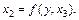
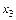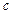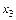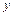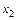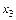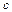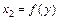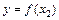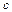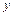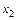Нехай в цих рівняннях дорівнює деякій довільній величині , тоді член, який відповідає змінній збігатиметься з вільним членом, а отже, дістанемо дві прості регресії, які відбивають загальну зміну і на площині = . Оскільки модель є лінійною, то коефіцієнти регресії і лишаються незмінними при різних значеннях , тобто можна стверджувати: квадрат коефіцієнта частинної кореляції між і дорівнює добутку коефіцієнтів при 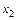і 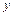у двох множинних регресіях.

Згідно з (8) запишемо ці рівняння у вигляді

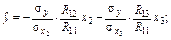
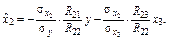
де — алгебраїчні доповнення до елемента 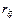матриці .

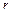Звідси

.

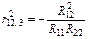Для знаходження частинного коефіцієнта кореляції змінної y з x ₂ за умови, що змінна x ₃ стала, достатньо взяти добуток параметрів при x ₂ і y в наведених щойно рівняннях з протилежним знаком.

Аналогічно

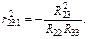
Тоді частинні коефіцієнти кореляції будуть такі:

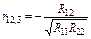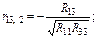
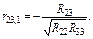; (15)

Ці висновки можна поширити на випадок, коли економетрична модель має 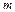незалежних змінних 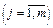, але при цьому решта незалежних змінних (крім двох) є константами.

Гіпотезу про рівень значущості зв’язку між залежною і незалежною змінними можна перевірити з допомогою F -критерію:

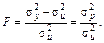(16)

При цьому ми виходимо з того, що залишки u розподілені нормально, тобто користуємося фундаментальною теоремою про те, що для нормально розподіленої випадкової величини 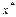з нульовою середньою і одиничною дисперсією сума квадратів її n випадково вибраних значень має розподіл 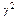з n ступенями свободи.

Дисперсії, які застосовуються для обчислення F -критерію, наведено в табл.2.

Фактичне значення F -критерію порівнюється з табличним при ступенях свободи n – m і m – 1 і вибраному рівні значущості. Якщо F факт > F табл, то гіпотеза про істотність зв’язку між залежною і незалежними змінними економетричної моделі підтвержується, у противному разі - відкидається.

Оскільки коефіцієнт кореляції є також вибірковою характеристикою, яка може відхилятись від свого “істинного” значення, значущість коефіцієнта кореляції також потребує перевірки. Базується вона на t -критерії

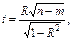
де 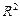— коефіцієнт детермінації моделі; 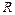— коефіцієнт кореляції; 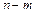— число ступенів свободи.

Якщо 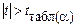, де 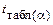— відповідне табличне значення t -розподілу з 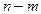ступенями свободи, то можна зробити висновок про значущість коефіцієнта кореляції між залежною і незалежними змінними моделі.

Перевіримо значущість оцінок параметрів В і знайдемо для них довірчі інтервали, припустивши для цього, що залишки u нормально розподілені, тобто 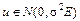. Тоді параметри моделі В задовольняють багатовимірний нормальний розподіл:

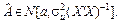(17)

Коли відома величина 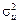, то цей результат можна бути використати для перевірки значущості елементів вектора 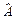та оцінювання довірчих інтервалів елементів цього вектора. Проте дисперсія 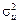невідома, а отже, потрібно розглянути методи її знаходження.

Для цього визначимо залишки:

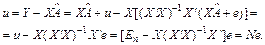(18)

Таким чином, залишки, які можна дістати на підставі експериментальних даних, записано у вигляді лінійних функцій від невідомих залишків 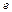. Тоді суму квадратів відхилень подамо у вигляді

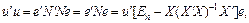(19)

де N — симетрична ідемпотентна матриця.

У цих перетвореннях ми виходили з того, що N є симетричною ідемпотентною матрицею, оскільки E_n — одинична матриця, а 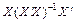— симетрична розміром n ´ m.

Знайдемо математичне сподівання для обох частин рівняння (19) і застосуємо спочатку властивість, яка полягає в тому, що 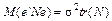, де 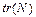— слід матриці N, а далі — властивість комутативності добутку матриць відносно операцій обчислення сліду матриці.

З огляду на сказане маємо:

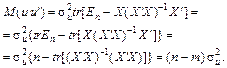(20)

У цьому співвідношенні матриця 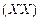має порядок 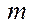, добуток 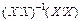дорівнює 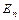, а її слід дорівнює . Звідси

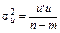. (21)

Співвідношення (21) дає нам незміщену оцінку дисперсії залишків.

Нарешті, лишилося показати, що сума квадратів залишків 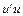розподілена незалежно від В. Для цього знайдемо коваріацію залишків:

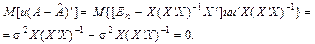(22)

Оскільки 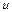і В є лінійні функції від нормально розподілених змінних, то вони також розподілені нормально і, як було показано, їх коваріації дорівнюють нулю.

Це дає нам змогу скористатися t -розподілом для перевірки гіпотез відносно істотності кожного з параметрів економетричної моделі

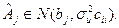
Перевірку гіпотези виконаємо згідно з t -критерієм:

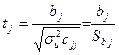, (23)

де — діагональний елемент матриці 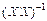. Знаменник відношення (23) 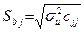— називається стандартною помилкою оцінки параметра моделі.

Обчислене значення t -критерію порівнюється з табличним при вибраному рівні значущості і 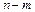ступенях свободи. Якщо t факт > t табл, то відповідно оцінка параметра економетричної моделі є достовірною.

На основі t -критерію і стандартної помилки побудуємо довірчі інтервали для параметрів :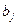

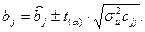(24)

Дата добавления: 2013-12-13