За результатами аналітичного групування

№ з/п	Групи банків за обігом коштів, млн.грн.	Кількість банків f	Середній прибуток, млн.грн.
	Разом

Міжгрупова дисперсия:

Середня з групових дисперсій:

Суть дисперсійного аналізу полягає у зіставленні (порівнянні) різних видів дисперсій: міжгрупової та загальної, загальної та внутрішньогрупової, міжгрупової внутрішньогрупової. У нашому прикладі вплив розміру обігу коштів банків як групуючого фактора на розмір прибутку майже у 10 разів (24,802:2,558=9,7) білыпий, ніж вплив інших випадкових факторів. Міжгрупова варіація становить 90,6 % у загальній варіації (24,802:27,36=0,906).

Для вимірювання тісноти (щільності) зв'язків між ознаками застосовується кореляційний метод, суть якого полягає у визначенні спеціальних співвідношень, що базуються на правилі додавання дисперсій.

Відшошення міжгрупової (факторної) дисперсії до загальної розглядається як міра щільності кореляційного зв'язку i називається коефіцієнтом детермінації.

За статистичною структурою це відношення є часткою варіації результативної ознаки у, яка пов'язана з варіацією ознаки х. Здобувши квадратний корінь із цього відношення, одержуємо емпіричне кореляційне відношення.

У нашому прикладі:

Таким чином, в обстеженій сукупності банків 95,21% варіації прибутку пов'язані з варіацією обігу коштів.

Кореляційне відношення змінюється від 0 до 1. Якщо η=0, то міжгрупова дисперсія дорівнює нулю. Це можливо лише за умови, коли всі грпові середні однакові i кореляційний зв'язок між ознаками відсутній. При η=l міжгрупова дисперсія дорівнює загальній, а середня з групових — нулю. В цьому випадку кожному значенню факторної ознаки відповідає єдине значення результативної ознаки, тобто зв'язок між ознаками функціональний.

Індекс кореляції визначають зіставленням внутрішньогруповoї i загальної дисперсії, i обчислюють за формулою:

Як бачимо величина R збіглася з показником η. Чим ближче R до 1, тим тісніший зв'язок між ознаками.

Слід підкреслити, що значення η² > 0 не завжди є доказом наявності кореляційного зв'язку між ознаками. Відмінне від нуля кореляційне відношення може з'явитись i при випадковому розподілі сукупності на групи.

Перевірка істотності відхилень групових середніх здійснюється за допомогою критеріїв математичної статистики. Вона грунтується на порівнянні фактичного значения η² з так званим критичним. Останнє є тим максимально можливим значенням кореляційного відношення, яке може виникнути випадково при відсутності кореляційного зв'язку. Якщо фактичне значення η² більше від критичного, то зв'язок між результативною i факторною ознаками вважається істотним. Якщо фактичне значения η² менше критичного, то наявність кореляційного зв'язку між ознаками не доказана i зв'язок вважається неістотним.

Для оцінки надійності кореляційних характеристик використовують критерії Фішера (F) або Стьюдента (t).

Критерій Фішера (F-критерій) визначається за формулою:

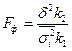
де σ² — міжгрупова дисперсія; — середня групова (залишкова) дисперсія; k₁ і k₂ — ступені вільності для великої i малої дисперсії. Фішер знайшов розподіл відношень дисперсії i розробив відпвідні математичні таблиці, в яких наводиться F – критерій теоретичний F_Т при двох ймовірностях 0,95 і 0,99. Якщо F_ф>Fт, то з прийнятим ступенем ймовірності можна стверджувати про наявність впливу фактора, який вивчається. Коли F_ф<Fт, то різниця між дисперсіями зумовлена впливом випадкових факторів.

Розподіл у таблицях Фішера для знаходження F_T залежить від ступенів вільності міжгрупової к₁ i середньої з групових к₂ дисперсій. В аналітичному групуванні їх обчислюють за формулами:

к₁ =m - 1 к₂ = n – m

де n — кількість елементів досліджуваної сукупності; m — число груп. За даними наведеного вище прикладу (табл. 10.6):

к₁ =m – 1 = 3 – 1 = 2; к₂ = n – m = 10 – 3 =7

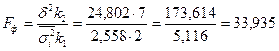
Знаходимо F_T при ймовірності 0,95 i даних ступенях вільності за математичною таблицею. Воно становить F_T(0,95) = 4,8.

Отже, F_ф > F_T(33,935 > 4,8), що свідчить про суттєвий вплив обігу коштів банків на їx прибуток.

Надійність кореляційного відношення за критерієм Стьюдента (t—критерію)

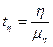
де µ_η - середня похибка кореляційного відношення.

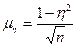
Якщо критерій Стьюдента t_n ≥ 3, показник кореляційного відношення вважають вірогідним (тобто зв'язок між досліджуваними явищами є доведеним). Якщо ж критерій t_n < 3, то висновки про вірогідність зв'язку між досліджуваними явищами сумнівні.

Комбінаційні аналітичні групування i дисперсійний аналіз використовують для вивчення зв'язку результативної ознаки з двома i більше факторними ознаками. Вони дають можливість аналізувати залежність результативної ознаки від кожного з факторів при фіксованих значеннях інших. Методи вимірювання такого зв'язку і перевірку його істотності називають багатофакторними дисперсійними комплексами. Вони пов'язані з громісткими розрахунками і потребують використання ЕОМ.

Дата добавления: 2013-12-14