І випуском продукції

№ підприємства	Випуск валової продукції, млн.. грн.. у	Yх
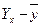
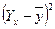
		20,294 20,294 25,353 27,882 30,412 27,882 32,941 35,471 38,000 35,471	-9,4 -4,4 -9,4 0,6 2,6 -4,4 -0,4 7,6 10,6 6,6	88,36 19,36 88,36 0,36 6,76 19,36 0,16 57,76 112,36 43,56	-9,106 -9,106 -4,047 -1,518 1,012 -1,518 3,541 6,071 8,600 6,071	82,919 82,919 16,378 2,304 1,024 2,304 12,539 36,857 73,960 36,857
Разом		294,00		436,4		348,061

Визначимо середній випуск продукції на одне підприємство:

Кореляційне відношення за даними розрахункових даних, наведених в таблиці 10.9, обчислимо за формулою:

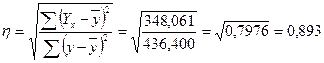або 89,3%

Для вимірювання щільності прямолінійих зв'язків використовується лінійний коефіцієнт кореляції. Найбільш зручною формулою для розрахунку коефіцієнта кореляції за незгрупованими даними є наступна:

У нашому прикладі (табл.10.8):

Коефіцієнт кореляції можна обчислювати i за іншими формулами. Зокрема:

;

Якщо визначена форма кореляційного зв'язку i обчислений коефіцієнт регресії а, то коефіцієнт кореляції можна обчислити за формулою:

Лінійний коефіцієнт кореляції може набувати любих значень в межах від до -1 до +1. Якщо r близьке до 1, то зв'язок між ознаками тісний, якщо r наближається до 0, то зв'язок незначний. Знак лінійного коефіцінта кореляції вказує напрямок зв'язку — знак плюс свідчить про прямий зв'язок, знак мінус — обернений зв'язок.

В нашому прикладі лінійний коефіцієнт кореляції свідчить про прямий зв'язок між показниками — обсяг випуску продукції на 89,3% залежить від вартості основних виробничих фондів i на 10,7% — від інших факторів.

Перевірку істотності зв'язку в кореляційно-регресійному аналізі здійснюють за допомогою тих самих критеріїв i за тими ж процедурами, що i в аналітичному групуванні та дисперсійному аналізі.

Для встановлення достовірності обчисленого кореляційного відношення скористаємося t — критерієм Стьюдента:

Оскільки t_η ^> t_t (13.33 > 3), залежність випуску продукції від вартості основних виробничих фондів є доведеною.

Дата добавления: 2013-12-14