Средний уровень в рядах динамики средних и относительных величин

Таблица 8– Производство молока и поголовье коров в хозяйстве во II квартале отчётного года

Месяц	Поголовье коров на начало месяца, гол.	Производство молока, ц	Процент выполнения плана	Средний месячный надой молока на 1 корову, ц
по плану	фактически
Апрель					16,8
Май					18,6
Июнь					19,2
Всего				99,6	18,2

Средний фактический объём производства

Средний процент выполнения плана =----------------------------------------------------------- =

Средний объём производства по плану

=;

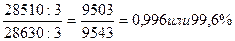Средний фактический объём производства

Средний надой молока на 1 корову =--------------------------------------------------------- =

Среднее поголовье коров

=;

Среднее поголовье коров =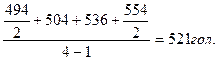

Рисунок 2– Типы колебаний в динамических рядах

ПРИЁМЫ ВЫЯВЛЕНИЯ ОСНОВНОЙ ТЕНДЕНЦИИ

Ø усреднение левой и правой половины ряда: ряд динамики разделяют на две части, находят для каждой среднее арифметическое значение и проводят через полученные точки линию тренда на графике.

Ø укрупнение периодов:

Ø сглаживание динамического ряда при помощи скользящей средней:

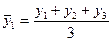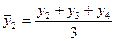; ;и т.д.

Таблица 9– Выравнивание суммы налогов, уплаченных в местный бюджет за 1999-2007 годы с помощью скользящей средней

Год	Фактическая сумма налогов, уплаченных в местный бюджет, млн. руб.	Сумма по скользящим трехлетиям	Средние скользящие
			632,0 661,7 667,3 674,0 675,7 700,7 685,0

Ø анализ цепных показателей ряда динамики:

а ) при постоянных цепных абсолютных приростах делается вывод о равномерном типе развития. Основная тенденция в этих рядах выражается уравнением прямолинейной функции y_t = a ₀ + a ₁ t, где

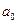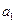и – параметры уравнения;

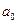– начальный уровень тренда в момент или период, принятый за начало отсчёта времени;

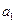– среднее абсолютное изменение за единицу времени;

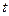– обозначение времени.

Параметр 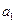определяет направление развития: если , то уровни ряда равномерно возрастают в среднем за единицу времени на величину 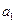, если , то происходит их равномерное снижение.

б) при постоянных темпах приростах делается вывод о равноускоренном или равнозамедленном типе развития, основная тенденция которого выражается уравнением параболы второго порядка: y_t = a ₀ + a ₁ t + a ₂ t ².

Значение параметров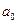и 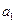идентично предыдущему уравнению.

Параметр 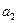характеризует изменение интенсивности развития в единицу времени. При происходит ускорение развития, при 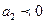– замедление развития.

Соответственно при параболической форме тренда возможны следующие варианты развития:

Ø если ; – ускорение роста;

Ø если ; 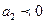– замедление роста;

Ø если ; 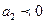– ускорение замедления;

Ø если ; – снижение замедления.

в ) при стабильных цепных темпах роста делается вывод о развитии по экпоненте, основная тенденция которого выражается уравнением показательной функции , где 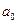– константа ряда, 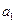–темп изменения в разах.

При 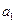>1 экспоненциальный тренд выражает тенденцию ускоренного и всё более ускоряющегося возрастания уровней, при 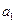<1 экспоненциальный тренд означает всё более замедляющегося снижения уровней динамического ряда.

г) при сокращении цепных абсолютных приростах в конечных уровнях ряда делается вывод о развитии с замедлением в конце периода, основная тенденция которого выражается уравнением логарифмической функции.Логарифмическая форма тренда применяется для отображения тенденции замедляющегося роста уровней при отсутствии предельно возможного значения, например, роста спортивных достижений, производительности агрегата, продуктивности скота.

д) развитие с переменным ускорением (замедлением), основная тенденция которого выражается уравнением параболы третьего порядка . Параметр 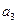отображает изменение ускорения (замедления):

Ø если ; ; – возрастающее ускорение роста;

Ø если ; ;– замедляющееся ускорение роста;

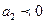Ø если ; ; – возрастающее замедление роста;

Ø если ; ; 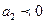– снижающееся замедление роста;

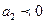Ø если ; ;– возрастающее ускорение замедления;

Ø если ; ;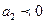– замедляющееся ускорение замедления;

Ø если ; ;– уменьшающееся снижение замедления

Ø если ; ;– возрастающее снижение замедления

е ) гиперболическая форма тренда y_t = a ₀ + a ₁ , применим для отображения тенденции процессов, ограниченных предельным значением уровня;

ж) тренд в форме степенной функции 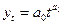, применим для отображения тенденции явлений с разной мерой пропорциональности изменений во времени;

з ) логистический тренд и др.

Ø аналитическое выравнивание динамического ряда: основная тенденция развития 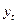рассчитывается как функция времени. В этом случае фактические (эмпирические) уровни заменяются теоретическими, вычисленными по соответствующему аналитическому уравнению.

При расчёте параметров трендовых моделей способом наименьших квадратов строятся и решаются системы нормальных уравнений:

для прямой линии для параболы 2-го порядка

.

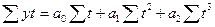
Способ отсчёта от условного начала

При чётном числе уровней динамического ряда «t» обозначают следующим образом:

и т.д.

-7

-5

-3

-1

и т.д.

При нечётном числе уровней динамического ряда «t» обозначают следующим образом:

и т.д.

-4

-3

-2

-1

и т.д.

В этом случае система уравнений упрощается и приобретает вид для уравнения прямой линии: для уравнения параболы:

å y = a ₀ n;

å yt = a ₁å t ².

Пример аналитического выравнивания по уравнению прямой линии

Таблица 10– Расчет данных для нахождения параметров уравнения прямой

Годы	Обозначение периода t	Фактическая сумма налогов, млн. руб. у	t^2	уt	Теоретическая (выровненная) сумма налогов
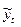
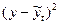
	-4			-2304	624,1	2313,6
	-3			-1923	634,0
	-2			-1358	643,9
	-1			-665	653,8	125,4
					663,7	32,5
	+1				673,6	645,2
	+2				683,5	182,2
	+3				693,4	1568,2
	+4				703,3	2631,7
Итого						8779,8

Подставим полученные суммы в систему уравнений:

;

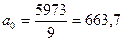Синтезированная модель тренда имеет вид:

Положительное значение параметра «а₁» указывает на тенденцию к росту суммы налогов, уплаченных в местный бюджет, в среднем ежегодно на 9,9 млн. рублей за период 1999-2007 годы.

Подставляя значение t в уравнение, рассчитаем теоретические уровни ряда:

для 1999 г. млн. руб.

для 2000 г. млн. руб.

и т. д.

Дата добавления: 2013-12-14