Показатели для измерения силы колебаний

Пример аналитического выравнивания по параболе второго порядка

Таблица 11–Расчет данных для нахождения параметров уравнения параболы второго порядка

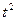
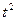
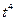
Годы	Фактич. сумма на-логов, млн. руб. (y)	Обоз-начение периода (t)		y t	y		Теоретич. сумма налогов, млн. руб.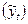
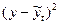
		-4		-2304			592,5	272,25
		-3		-1923			629,2	139,24
		-2		-1358			653,1	670,81
		-1		-665			673,2	67,24
							686,5	812,25
		+1
		+2					692,7	515,29
		+3					685,6	2246,76
		+4					671,7	388,09
Итого								5147,93

Поставим полученные суммы в систему уравнений:

663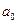,7= + 6,7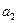

646,2= 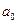+11,8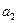

17,5= -5,1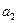

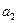= -3,4

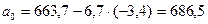
Таким образом, уравнение параболы второго порядка характеризующее тенденцию изменения налогов, уплаченных в местный бюджет хозяйствующими субъектами, имеет вид:

.

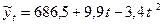При данных значения параметров (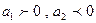) основная тенденция характеризуется как замедленный рост.

Параметр «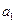» характеризует средний ежегодный размер увеличения суммы налогов в анализируемый период – 9,9 млн. рублей; скорость замедление роста суммы налогов при нечетном числе уровней составляет 2 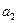- 6,8 млн. рублей.

Определим величину стандартной и относительной ошибки аппроксимации, используя данные последней графы таблиц 10 и 11:

;

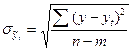для линейного тренда:

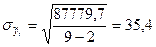млн. руб.;

.

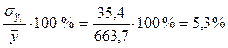для параболического тренда:

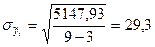млн. руб.

.

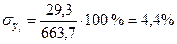Сравнив полученные значения ошибок для уравнений прямой и параболы второго порядка, можно сделать вывод о том, что парабола более точно описывает основную тенденцию ряда динамики суммы налогов, уплачиваемых хозяйствующих субъектов в местный бюджет.

Ø амплитуда отклонений или размах колебаний:

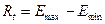, где

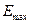– максимальное положительное отклонение уровней от тренда;

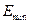– максимальное отрицательное отклонение уровней от тренда.

Ø среднее абсолютное отклонение:

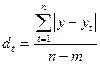, где

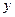– фактический уровень ряда динамики;

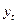–теоретический уровень ряда динамики;

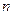– число уровней;

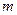– число параметров в модели тренда.

Ø среднее квадратическое отклонение:

.

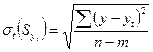Ø относительное линейное отклонение:

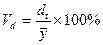
Ø коэффициент колеблемости:

.

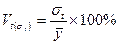Ø показатель устойчивости (коэффициент алиенации):

.

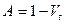Дата добавления: 2013-12-14