Уравнение Бернулли для элементарной струйки идеальной жидкости

Рассмотрим установившееся течение идеальной жидкости, находящейся под действием лишь одной массовой силы - силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.

Возьмем одну из элементарных струек, составляющих поток, и выделим сечениями 1 и 2 участок этой струйки произвольной длины (рис. 10). Пусть площадь первого сечения равна dS ₁, скорость в нем 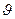₁, давление p ₁, а высота расположения центра тяжести сечения, отсчитанная от произвольной горизонтальной плоскости сравнения, z ₁. Во втором сечении соответственно dS ₂, 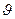₂, р ₂ и z ₂.

За бесконечно малый отрезок времени dt выделенный участок струйки переместится в положение 1' - 2'.

Применим к массе жидкости в объеме участка струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого тела. Такими силами в данном случае являются силы давления, действующие нормально к поверхности рассматриваемого участка струйки, и сила тяжести. Подсчитаем работу сил давления, силы тяжести и изменение кинетической энергии участка струйки за время dt.

чении положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы p ₁ dS на путь 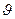₁ dt:

p ₁ dS _{1 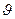1} dt.

Рис. 10. Схема для вывода уравнения Бернулли

Работа силы давления во втором сечении имеет знак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением

- p ₂ dS _{2 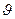2} dt.

Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности а следовательно, нормальны и к перемещениям.

Итак, работа сил давления будет равна

p _{1 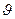1} dS ₁ dt - p _{2 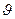2} dS ₂ dt.

Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, поэтому надо из энергии положения жидкости в объеме 1 - 2 вычесть энергию положения жидкости в объеме 1' - 2'. При этом энергия положения промежуточного объема 1' - 2 сократится, и останется лишь разность энергий элементов 1 - 1', 2 - 2'. Если учесть уравнение расхода (15), то нетрудно заметить, что объемы, а следовательно, и силы тяжести заштрихованных элементов 1 - 1' и 2 - 2' равны между собой:

.

Тогда работа силы тяжести выразится как произведение разности высот на силу тяжести :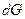

.

Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема 1' - 2' вычесть кинетическую энергию объема 1 - 2. При вычитании кинетическая энергия промежуточного объема 1' - 2 сократится, и останется лишь разность кинетических энергий элементов 2 - 2' и 1 - 1', сила тяжести каждого из которого равна dG.

Таким образом, приращение кинетической энергии равно

.

Сложив работу сил давления с работой силы тяжести и приравняв эту сумму приращению кинетической энергии получим

.

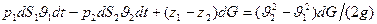Разделим это уравнение на dG, и произведя сокращения, получим

.

Сгруппируем члены, относящиеся к первому сечению, в левой части уравнения, а члены, относящиеся ко второму сечению, в правой:

, (16)

где z - геометрическая высота, или геометрический напop; p/(ρg) - пьезометрическая высота, или пьезометрический напор; - скоростная высота, или скоростной напор.

Полученное уравнение называется уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Оно было выведено Даниилом Бернулли в 1738 г.

Трехчлен вида

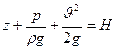
называется полным напором.

Уравнение Бернулли (16) записано для двух произвольно взятых сечений струйки и выражает равенство полных напоров H в этих сечениях. Так как сечения взяты произвольно, следовательно, и для любого другого сечения этой же струйки полный напор будет иметь то же значение:

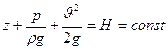(вдоль струйки)

Итак, для идеальной движущейся жидкости сумма трех напоров (высот): геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.

Дата добавления: 2013-12-14