Распределение Пуассона

Отрицательное биномиальное распределение

Биномиальный закон распределения

Гипергеометрическое распределение

В партии N изделий, среди них M стандартных. Случайно отбирается n изделий (без возврата – формула Бернулли не применима). X –СВ, число m стандартных изделий из n отобранных.

X=m, => 0,1,2,…, min{M,n}

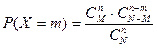
Биномиальным называют закон распределения дискретной СВ X – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p (а не появления соответственно q). Распределение вероятностей определяется формулой Бернулли.

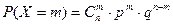
m – число раз появления события

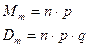
Описывает распределение СВX – числа испытаний в схеме Бернулли до k-го интересующего события (включая последнее испытание).

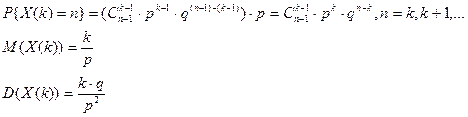
Введем распределение Пуассона через биномиальное распределение. Заданы n, p, q = 1-p. При этом p <= 0.1 (вероятность появления события очень мала), а n достаточно велико. Введем допущение: 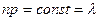, то есть среднее число появления события в различных сериях испытаний (различные значения n)остается неизменным.

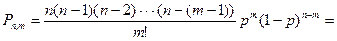
{так как 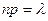, то } =

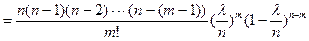
т.к. n – велико, существуют определенные трудности вычисления P_n,m. Перейдем к приближенному определению как предельному значению, к которому стремиться данное соотношение.

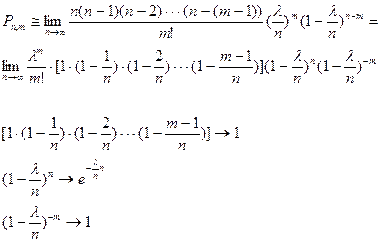
таким образом получаем:

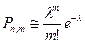
Распределение Пуассона имеет смысл для массовых, редких событий!!

Для этого распределения характерно: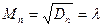

На практике распределение Пуассона используется:

1. Для приближенного вычисления вероятностей Pn,m биномиального закона распределения при достаточно больших n и p <= 0.1.

2. для характеристики распределения простейшего потока событий во времени

Поток событий – последовательность событий, наступающих в случайные моменты времени.

Простейший пуассоновский поток событий – поток событий, обладающий свойствами стационарности, отсутствия последействия и ординарности.

Стационарность – вероятность появления K событий за промежуток времени длительностью t, есть функция, зависящая только от K и длительности t, но не зависит от начала его отсчета. Иначе,: интенсивность потока событий во времени есть величина постоянная ().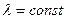

Интенсивность потока – среднее число событий появляющихся в единицу t.

Отсутствие последействия – вероятность появления K событий на любом промежутке t не зависит от того сколько раз оно появлялось в предшествующие моменты. То есть предыстория процесса не оказывает влияния на наблюдаемый процесс, или имеет место взаимная независимость появлений того или иного числа событий в непересекающихся промежутках времени.

Ординарность – появление 2-х и более событий за бесконечно малый промежуток t практически невозможно. То есть за бесконечно малый промежуток времени появляется не более одного события.

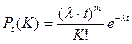, где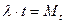

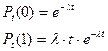
Дата добавления: 2013-12-14