Закон Гука. Исследования твердых тел показали, что в большинстве случаев деформации растяжения-сжатия в определенных пределах пропорциональны действующим силам

Исследования твердых тел показали, что в большинстве случаев деформации растяжения-сжатия в определенных пределах пропорциональны действующим силам. Этот закон пропорциональности напряжения и деформации установил современник Ньютона Роберт Гук и в настоящее время он записывается в виде

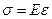, (2.2)

где Е – модуль продольной упругости (модуль Юнга), определенный как отношение нормального напряжения к соответствующей относительной линейной деформации стержня; - относительная линейная деформация растяжения-сжатия при одноосном напряженном состоянии для образца первоначальной длиной l; Δ l – удлинение (укорочение) стержня под действием приложенной силы.

Одновременно с продольной деформацией наблюдается и деформация бруса в направлениях, перпендикулярных его оси – поперечные деформации. Если обозначить через b характерный размер поперечного сечения, то поперечная деформация при растяжении определяется уравнением

.

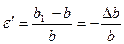Поперечные и продольные относительные деформации связаны между собой зависимостью

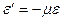, (2.3)

где μ < 1 – коэффициент Пуассона.

В таблице 2.2 приведены значения модулей упругости и коэффициентов Пуассона для основных конструкционных материалов.

Таблица 2.2

Модули продольной упругости

Наименование материала	Модуль упругости Е, МПа	Коэффициент Пуассона
Сталь углеродистая Чугун Сплавы алюминия Медь	2,1 ∙ 10^5 (1,15 – 1,6) ∙ 10^5 0,72 ∙ 10^5 (1,0 – 1,3) ∙ 10^5	0,24 – 0,30 0,23 – 0,27 0.26 – 0,36 0,31 – 0,34

В соответствии с уравнениями (2.1) и (2.2) абсолютная величина упругой деформации стержня постоянного сечения под действием осевой нагрузки F определяется зависимостью

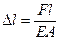, (2.3)

где А – площадь поперечного сечения стержня.

Дата добавления: 2013-12-14