Аксиомы статики

Введение. Основные понятия.

Аксиомы статики.

Основы теоретической механики.

Литература

1. Джамай В.В. и др. Прикладная механика. М.: Юрайт, 2012.

2. Рощина Г.И., Самойлова Е.А. Детали машин и основы конструирования. М.: Юрайт, 2012.

3. Сурин В.М. Прикладная механика. М.: Новое знание, 2008.

4. Бегун. П.И., Кормилицын О.П. Прикладная механика. М.: Политехника, 2006.

5. Махова Н.С., Поболь О.Н., Семин М.И. Основы теории механизмов и машин. М.: Владос, 2006.

6. Андреенков Е.В., Сёмин М.И., Харитонов Г.И. Основы деталей машин. М.: Владос, 2007.

1. Вереина Л.И., Краснов М.М. Техническая механика. М.: Академия. 2012.

8. Хруничева Т.В. Детали машин: Типовые расчеты на прочность. М.: ИД «Форум» - «Инфра-М», 2012.

Прикладная механика (ПМ) является частью общей области науки - машиноведения и занимается изучением движения и работы ме­ханизмов, совершенствованием расчетов и оценок прочности и триботехнической надежности основных элементов машин и механизмов, обобщением инженерного опыта создания механизмов и машин. Предметом курса ПМ являются элементы машиностроительных конструкций. Цель – изучение основ современных методов расчета и конструирования деталей машин и механизмов.

Основные части курса ПМ

Основы теоретической механики. Изучают законы взаимодействия, равновесия и движения материальных тел.

Основы сопротивления материалов. Наука о прочности, жесткости устойчивости элементов конструкций. Конечной задачей является расчет надежных и наиболее экономичных в отношении размера и весашей машин и конструкций.

Основы теории механизмов и машин. Изучают структуру, т.е.: строение, кинематику и динамику механизмов и машин в связи с их анализом и синтезом. Анализ - изучение существующих механизмов. Синтез - проектирование новых механизмов.

Основы проектирования деталей, узлов и механизмов машин, приборов и аппаратов. Изучают условия работы, основы расчетов и конструирования деталей общего назначения, которые встречаются фактически в любой машине.

Ни одна наука не обходится без абстракций, идеализированных схем реальных явлений. Расчетной схемой является абстракция реальных явлений, когда вводят некоторые упрощающие предположение и не учитывают те или иные малозначащие факторы. Важнейши­ми для статики являются две абстракции: материальная точка и абсолютно твердое тело.

Материальной точкой называют геометрическую точку (без размеров), обладающую бесконечно малой или конечной массой. Абсолютно твердым телом называют систему, у которой расстояния между любымиыми двумя точками постоянны.

В природе и технике не существуют ни материальные точки абсолютно твердые тела. Понятием «материальная точка» можно пользоваться во всех случаях, когда форма и размеры тел несущественые, а основным является учет массы тела, например, при изучении паления тел а пустоте, при вычислении количества движения тел, кинетической энергии поступательно движущегося твердою тела и т.д. В этих случаях тело заменяют геометрической точкой, как правило, это центр тяжести тела, и считают, что в ней сосредоточена вся масса.

С абстракцией «абсолютно твердое тело» мы встречаемся в тех явлениях, для которых масса, формы и размеры тела существенны но изменения формы - деформации настолько малы, что ими можно пренебречь. Используя методы статики абсолютно твердого тело и сопротивлении материалов определяют реакции опор (противодействий) на жесткие балки, пренебрегая малыми деформациями, прогибами.

Изолированной называют материальную точку, которая не подвергается действию других материальных точек. (В природе таковой нет, т.к. везде присутствуют гравитационные поля).

Движением но инерции называют прямолинейное и равномерное движение точки. Состоянием равновесия точки или просто равновесием называют ее состояние покоя или движение по инерции.

В основу статики положено несколько аксиом, полученных в результате многовековых наблюдений и научных обобщений. Закон инерции: всякая изолированная материальная точка на- ходится в равновесии, пока какая – нибудь причина не выведет его из чтого состояния. Из этой аксиомы следует понятие силы, как причины, изменяющей состояние покоя пли движения данного тела. В системе СИ за единицу силы принята сила, называемая Ньютоном и обозначаемая Н. О силах судят по их действиям. Эквивалентными считают те силы, которые будучи приложены но отдельности к одному и тому же телу, произведут на его одинаковое действие. Сила - величина векторная, т.к. действие одного тела па другое существенно зависит от направления. Например, если с одной и той же по модулю I силой будем давить сверху вниз на спинку стула, то стул останется в покое, если стул тянут в вверх с силой, больше его веса, го стул будет подниматься, а если силу приложить горизонтально - стул опрокинется. Т.к. во всех Этих случаях действия сил разные, следовательно, и силы разные, несмотря на то, что их модули могут быть одинаковы. Сила, приложенная к твердому телу - вектор несвободный, т.к. ее действие зависит от точки приложения. Например, если не меняя величи­ны силы и ее направления, параллельно полу, потянуть стул за спинку назад, то стул опрокинется, а если потянуть за основание ножки непос­редственно около пола, то стул будет скользить по полу.

Итак, действие силы на твердое тело определяется величиной (модулем), направлением и точкой приложения. Силу, как и другие вектор­ные величины, изображают в виде направленного отрезка. Системой сил называют совокупность нескольких сил, приложенных к матери­альной точке или телу. Если точка или абсолютно твердое тело под действием системы сил находится в равновесии, то такую систему сил называют уравновешенной или эквивалентной нулю.

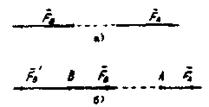
Простейшая уравновешенная система сил определяется второй аксиомой. Абсолютно твердое тело только тогда находится в равно­весии под действием двух сил, если эти силы равны по модулю и направлены в противоположные стороны по прямой, соединяющей точки приложения этих сил (Рисунок 1. а).

_, т.п. по модулю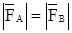

Аксиома третья. Действие системы сил на абсолютно твердое тело не меняется от присоединения или исключения уравновешенной системы сил.

Из приведенных аксиом следует теорема: сила, приложенная к абсолютно твердому телу, является вектором скользящим, т.е. не изме-няя действия силы на абсолютно твердое тело, можно ее прикладывать в произвольной точке по линии действия силы (Рисунок 1. б).

В т. А приложена сила , в т.В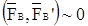, причем 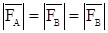по модулю

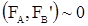
модулю.

Согласно 2 и 3 аксиомам от присо­единения этих сил действие силы не из­менилось, т.е. 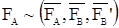. Но согласно аксиоме 2 имеем уравновешен­ную систему

Рис 1.

и, применяя вновь аксиому 3, исключаем эту сис­тему. Получаем F_A ~ F_B. Силу Fв можем рассматривать как силу

F_A, но только проскользнувшую по линии действия из точки А в точку В.

Итак: действие силы на абсолютно твердое тело определяется модулем, линией действия и направлением силы. Равнодействующей системы сил называют силу, действие которой заменяет собой дей­ствия данной системы сил. Замену одной силы несколькими называют разложением данной силы на составляющие.

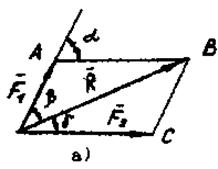
Аксиома четвертая (правило параллелограмма): равнодейству­ющая двух сил, приложенных в точке, приложена в той же точке и равна по величине и направлению диагонали параллелограмма, пост­роенного на этих силах, как на сторонах (Рисунок 2 а). Параллелог­рамм строят в определенном масштабе, т.е. выбранная единица соот­ветствует единице силы.

Если силы взаимно перпендикулярны F₁ ^ F₂ , т.е. a=90⁰, согласно

теореме Пифагора имеем: .

Аксиома пятая (закон действия и противодействия): две мате­риальные точки действуют друг на друга силами, равными по модулю и направленными в противоположные стороны по прямой, соединяю­щей эти точки (Рисунок 2 б).

Ньютон так это сформулировал: действие всегда равно и прямо противоположно противодействию:

Рис 2.

Из аксиомы 5 следует, что силы всегда встречаются попарно, т.е. все силы носят характер взаимодействий.

Изменяемой системой материальных точек называют такую со­вокупность точек, в которой расстояния между точками системы мо­гут изменяться. Согласно шестой аксиоме: равновесие изменяемой системы сил не нарушится, если система станет неизменяемой. Де­формируемое тело является изменяемой системой материальных то­чек. Применительно к нему 6-я аксиома носит название принципа от­вердевания: если деформируемое тело находится в равновесии под

действием некоторой системы сил, то равновесие не нарушится, если это тело станет абсолютно твердым. Принцип отвердевания широко используется в инженерных расчетах.

Дата добавления: 2013-12-14