Простейшие движения твердого тела

Поступательное движение. Поступательным называют такое движение твердого тела, при котором все прямые, соединяющие лю­бые две точки тела, перемещаются параллельно своим первоначаль­ным положениям.

Проведенная в теле прямая АВ во время движения перемещается параллельно своему начальному положению. Рассмот­рим перемещение тела за малый промежуток времени Δt. При этом можно считать, что точки А и В перемещаются по прямолинейным и параллельным прямым. За время Δt они пройдут одинаковые пути Δs. Следовательно, скорости этих точек будут одинаковы по величине v_A = v_B = v = ds/dt и направлены в одну сторону. Аналогично доказыва­ется равенство ускорений точек тела при поступательном движении: а_А = а_В = а.

Следовательно, при поступательном движении твердого тела все его точки описывают одинаковые траектории и в любой момент вре­мени имеют равные по величине и параллельно направленные ско­рости и ускорения.

Вращение твердого тела вокруг неподвижной оси. Вращением твердого тела вокруг неподвижной оси называют такое движение тела, при котором все его точки, лежащие на оси вращения, остаются неподвижными. Траектории всех остальных точек тела- окружности, плоскости которых перпендикулярны оси вращения, а центры лежат на этой оси. Представим себе, что плоскость II неизменно скреплена с телом, а плоскость I неподвижна, причем угол между этими плоскостями равен нулю при t = 0. Считая, что расположение тела по отношению к плоскости II известно, мы будем знать положение тела по положению плоскости II, которая определяется углом поворота тела φ, поэтому равенство 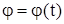является законом, или уравнением вращательного движения тела.

При вращении твердого тела вокруг неподвижной оси первую производную по времени от угла поворота тела называют его угловой скоростью: .

Угловая скорость измеряется в радианах в секунду, т.е. в рад/с, 1/с или с^{- 1}.

Равномерным называют такое вращение твердого тела, для которого величина угловой скорости постоянна: .

В технике, вместо угловой скорости, иногда вводят частоту вращения, которая измеряется числом оборотов в минуту. Угловая скорость для равномерного вращения является углом поворота в единицу времени. За один оборот тело описывает угол 2π рад, а если тело сделает n об/мин, то за минуту оно опишет угол 2 π n рад. Отсюда следует, что за 1 с угол поворота тела будет в 60 раз меньше:

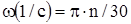
При вращении твердого тела вокруг неподвижной оси первую производную по времени от угловой скорости тела или вторую производную от угла поворота по времени называют его угловым ускорением:

или 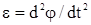, 1/с²

Равнопеременным называют такое вращение твердого тела, при котором величина углового ускорения постоянна: Интегрируя и считая, что при t₀=0, , получаем

,

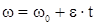Из предыдущих уравнений следует: 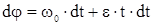. Интегрируем еще раз при начальном условии t₀ = 0, 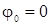и получаем:

.

Установим связь между линейными скоростями и ускорениями различных точек вращающегося тела с угловыми скоростью и ускорением этого тела.

Из математики известно, s = rгде r - радиус окружности, равный расстоянию точки от оси вращения, s - путь, пройденный точкой по дуге окружности, а φ - центральный угол, соответствующий дуге s и выраженный в радианах, тогда линейная скорость вращающегося тела:

v = ds/dt = r (dφ/dt) = r·ω.

Касательное ускорение точек вращающегося тела:

a_t = dv/dt = r (dω /dt) = r·ε.

Нормальное ускорение точек вращающегося тела:

a_n = v²/r = (r·ω)²/r = r·ω².

Полное ускорение:

.

Вектор полного ускорения точек вращающегося тела можно определить по углу а, образованного этим вектором с радиусом:

tgα = a_t/a_n = r·ε/ r·ω² = ε/ ω².

Дата добавления: 2013-12-14