Тогда результирующее напряжение

Напряжения изгиба

,

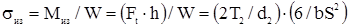где ; .

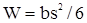Напряжения сжатия можно не учитывать.

.

; ,

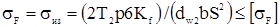где ,, ;

S_F - коэффициент безопасности;

K_F - коэффициент нагрузки, учитывающий реальные условия работы колес. По аналогии с расчетом на контактную прочность

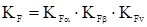
Размеры и форма зубьев зависят от модуля и числа зубьев. Размерные величины h и S неудобны для расчетов. Их удобнее выразить через безразмерные коэффициенты и модуль:

; ;

;

- коэффициент формы зуба.

Учитывая, что

для прямозубых колес ;

для косозубых колес .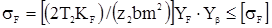

Формулы для проверочного расчета зубчатых передач.

Величина коэффициента формы зуба Y_F выбирается из таблицы в зависимости от числа зубьев прямозубого зубчатого колеса или по эквивалентному числу зубьев 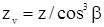для косозубых колес.

Y_β- коэффициент, учитывающий наклон зубьев ≈ cos β.

При проектном расчете открытых передач па прочность определяется модуль передачи, т.к. модуль является основным параметром, определяющим размеры чуба и, следовательно, его прочность.

Для прямозубых колес:

,

откуда 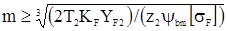или

, мм

- формулы для проектного расчета открытых зубчатых передач. При определении модуля сначала определяют отношение

[σ_F1]/Y_F1 и [σ_F2]/Y_F2 и меньшее из значений подставляют в формулу.

Полученный расчетный модуль округляют до стандартного. Число зубьев фактически выбирается в пределах:

z₁ = 20...24 - тихоходные передачи,

z₁ = 26...30 - быстроходные.

z₂ = z₁ • u, модуль m > 2...3 мм.

В открытых передачах зубья изнашиваются более интенсивно, чем в закрытых. Поэтому в формулы вводится коэффициент износа γ = 1,25... 1,5, тогда

, мм.

3.7 Конические зубчатые передачи.

Применяются для передачи движения между пересекающимися валами. Угол пересечения может изменяться от 10°<Σ<170°. Конические колеса дороже в изготовлении и сложнее в монтаже. Несмотря на это имеют широкое применение.

3.7.1 Геометрия конических зубчатых колес.

При построении проводим оси 1 и 2 валов. Строим δ₁ и δ₂ - углы наклона образующих I и II конусов. Длина образующей ограничивается так называемым внешним конусным расстоянием (Рисунок 74)

Рис 74.

,

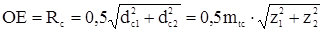где m_tc - внешний окружной модуль, являющийся стандартным. Конусы ОЕЕ₁, и ОЕ₁Е₂ - называются основными или начальными конусами. При вращении зубчатых колес эти конусы перекатываются друг по другу без скольжения аналогично начальным окружностям цилиндрических зубчатых колес.

От точки Е отложим длину зуба - точку С, отношение

называется коэффициентом длины зуба но конусному расстоянию, По ГОСТ 12289-76 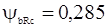, тогда . Из точки Е и Е₁ опустим перпендикуляры к образующим до пересечения с осями валов и получим новые конусы ЕЕ₁О₂ и Е₁Е₂О₄.

Конус О₂ЕЕ₁ называется наружным дополнительным конусом. Он строится таким образом, что его образующие перпендикулярны образующим основного конуса, основание совпадает с основанием основного конуса, а вершина лежит на оси вращения. Размеры, относящиеся к внешнему торцевому сечению, сопровождают индексом «е» R_e, d_e.

.

Продолжим образующую О₂Е и отложим значение внешнего окружного модуля m_tc, т.е. получим высоту головки зуба - точку К.

так же на продолжении О₂Е₁ получим точку К₁, точки К и К₁ соединим с точкой О. ОК и ОК₁ - называются образующими конуса выступов. Отложим по ЕО₂ отрезок ЕК₂ = 1,25 m_tc на и на Е₁О₂ отрезок .

ОК₂ и ОК₃ - называются образующими конуса впадин. Соединим точки С и С₁, с точкой О₃. Получим О₃С₁С - внутренний дополнительный конус.

В результате построения получим зуб конического колеса, который ограничивается подлине образующими наружного и внутреннего дополнительных конусов, по высоте - образующими конуса выступов и конуса впадин.

Дополнительные конусы ЕЕ₁О₂ и E₁E₂О₁ характеризуются тем, что в плоскости их образующей зубья перекатываются без скольжения и имеют стандартный параметр. Т.к. зубья конических колес имеют разную высоту по длине, то проектирование их ведется по одному заранее обусловленному показателю.

У прямозубых конических колес это размер на внешнем (большем) торце, где удобнее производить измерения. У непрямозубых - в средней точке, точке М.

Передаточное число

,

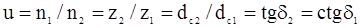где δ₁ и δ₂ - половины углов при вершинах начальных конусов.

Диаметры окружностей внешних начальных конусов

;

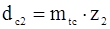Диаметры окружностей конусов выступов

,

;

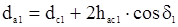Диаметры окружности конусов впадин

,

;

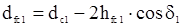Средние диаметры

,

.

Понятие о приведенном (эквивалентном) зубчатом колесе (Рисунок 75).

Действительные профили зубьев конических колес весьма близки к профилям зубьев воображаемых приведенных цилиндрических колес с радиусами начальных окружностей, равным длинам образующих дополнительных конусов.

, , , ,

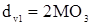d_v1 - диаметр приведенного (эквивалентного) колеса.

Определим диаметр окружности среднего конуса через d_c1

, .

Так как ; .

Модуль в среднем сечении

.

Рис 75.

Параметры приведенного колеса

.

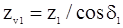
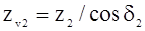3.7.2 Силы, действующие в зацеплении.

В зацеплении действуют три силы. Окружные силы

.

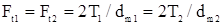Сила нормального давления .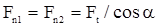

Радиальная сила приведенною .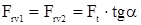

Радиальная сила первою колеса уравновешивается осевой силой второго колеса .

Осевая сила первого колеса уравновешивается радиальной силой второго колеса .

3.7.3 Особенности расчета конических передач на выносливость по контактным напряжениям.

Цель расчета: Предупредить выкрашивание рабочих поверхностей зубьев. Исходная формула Герца-Беляева

.

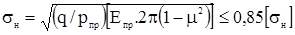Учитывая консольное расположение колес допускаемые контактные напряжения принимают на 15% меньше.

Для закрытых передач расчет выполняется для колеса как проектный, то есть определяется d_е2 - диаметр окружности внешнего начального конуса колеса.

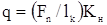- интенсивность нормальной силы (удельная нагрузка на единицу длины).

Сила нормального давления

.

- коэффициент нагрузки, учитывающий реальные условия работы (аналогично цилиндрическим передачам).

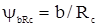- коэффициент длины зуба по конусному расстоянию = 0,285;

l_k -длина контактных линий;

К_c - коэффициент, учитывающий суммарную длину контактных линий;

ε_α - коэффициент торцевого перекрытия для косозубых колес.

Итак ; - приведенный модуль упругости, учитывающий материал обоих колес, при Е₁ = Е₂; Е_пр = Е₁ = Е₂; для стали .

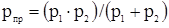- приведенный радиус кривизны профиля. Подставим в формулу Герца выражение, определяющее интенсивность нормальной силы, а также коэффициенты нагрузки, формы зуба, коэффициент, учитывающий механические свойства материала и коэффициент, учитывающий суммарную длину контактных линий, после преобразования получим при Σ = 90^о:

,

где z_н z_Е z_ε - коэффициенты, учитывающие соответственно форму сопряженных поверхностей, механические свойства материалов колес и суммарную длину контактных линий.

Частный вид формулы для стальных зубчатых колес

, при α = 20°; .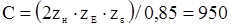

- формула для проверочного расчета стальных конических зубчатых колес на выносливость но контактным напряжениям.

При проектном расчете определяется d_e2 - диаметр окружности внешнего начального конуса колеса, чтобы освободиться от радикала, возведем в квадрат вышеприведенное неравенство:

.

Откуда

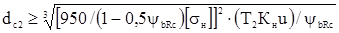, мм

- формула для проектного расчета конических передач.

Расчетное значение d_е2 округляется до ближайшего большего стандартного значения.

3.7.4 Особенности расчета конических передач на выносливость по напряжениям изгиба.

Этот расчет выполняется как проверочный с целью предупредить поломку зубьев.

В плоскости приведенного зубчатого колеса рассмотрим силы, действующие на зуб (Рисунок 76. а).

В точку М на середине зуба по линии нормального зацепления действует сила нормального давления. Перенесем силу по линии действия на ось симметрии и разложим ее. Опасное сечение представляет собой трапецию (Рисунок 76. б):

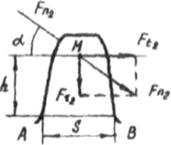
а)

б)

Рис 76.

АВ - опасное сечение, оно будет под точкой М в середине зуба. Центр тяжести у трапеции не в середине, а на расстоянии 0,4 b oт большего основания, т.к. мы рассчитываем несколько ослабленное сечение (т.е. середину зуба), то компенсируем это тем, что уменьшены на 15% [σ]_F, т.е. примем 0,85 [σ]_F, и в дальнейшем считаем опасное сечение прямоугольным с шириной S и длиной b. Аналогично цилиндрическим колесам, зубья конического колеса рассчитываются по результирующему напряжению ору основания зуба, равному разности изгибающих и сжимающих напряжений:

.

Напряжения изгиба

,

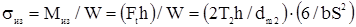где ; .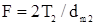

Напряжение сжатия .

,

где - коэффициент нагрузки, учитывающий реальные условия (аналогично цилиндрическим передачам).

Учитывая, что , по аналогии с цилиндрическими передачами - формула для проверочного расчета конических колес на изгиб, , где m_tm - средний модуль; m_tc - торцевой модуль.

Коэффициент формы зуба - выбирается из таблиц

в зависимости от приведенного числа зубьев

;

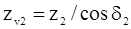
При проектном расчете открытых конических передач определяется модуль в среднем сечении.

Примем 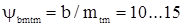- коэффициент длины зуба по модулю, тогда ,

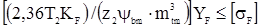откуда .

При определении модуля сначала определяются отношения 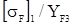и 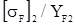и меньшее значение подставляется в формулу.

Полученный расчетный модуль округляется до ближайшего большего стандартного.

В открытых передачах зубья изнашиваются более интенсивно, чем в закрытых, поэтому в формулу вводится коэффициент износа, учитывающий снижение прочности γ = 1,25... 1,5:

.

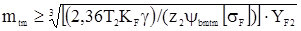3.8 Червячные передачи.

Применяются для передачи вращающего момента между валами, у которых угол скрещивания осей обычно составляет 90° (Рисунок 77.).

Червячная передача - это винтовая передача, у которой ведущее звено - червяк имеет 1...4 заходов (витков), а ведомое - червячное колесо > 28 зубьев.

В большинстве случаев ведущим является червяк, т.е корткий винт с трапецеидальной или близкой к ней резьбой.

Если червячное колесо представляет собой цилиндрическое косозубое колесо, то зубья имеют точечный контакт, малую нагрузочную способность и повышенный износ (Рисунок 77. а).

Наиболее широко распространены колеса с зубьями дугообразной формы, которые охватывают червяк по дуге с углом 2γ = 60... 110°.

При этом возникает линейный контакт, следовательно, повышается нагрузочная способность передачи (Рисунок 77. б).

Рис 77.

Параметрам червяка приписывается индекс -1.

Параметрам колеса - 2.

Достоинства червячной передачи:

1) Плавность и бесшумность работы;

2) Компактность;

3) Возможность получения больших передаточных чисел (до 1000);

4) Возможность получения самотормозящей передачи.

Недостатки:

1) Низкий KПД вследствие скольжения;

2) Значительное выделение тепла;

3) Применение ДЛЯ венцов червячных колес дефицитных антифрикционных материалов;

4) Повышенный износ колес.

Применяются червячные передачи при небольших и средних мощностях до 50 кВт, предпочтительно в приводах периодического действия (во избежание перегрева).

3.8.1 Классификация червячных передач.

В зависимости от формы внешней поверхности червяка передачи бывают с цилиндрическим или с глобоидным червяком.

Глобоидная передача имеет повышенный КПД более надежна и долговечна, но из-за сложности изготовления имеет ограниченное применение.

В зависимости от направления винтовой линии резьбы червяка передачи бывают с правым или левым червяком. Наибольшее применение имеют правые червяки.

В зависимости от числа заходов резьбы червяка передачи бывают с однозаходным или многозаходным червяками.

В зависимости от расположения червяка относительно колеса передачи бывают с нижним, верхним и боковым червяком.

При V₁ ≤ 4 м/с - нижний червяк.

При V₁ > 4 м/с - верхний червяк.

В зависимости от формы винтовой поверхности резьбы цилиндрического червяка передачи бывают с архимедовым, конволюнтным и эвольвентными червяками. Каждый из них требует различных способов нарезания.

3.8.2 Геометрия червячного зацепления (основные параметры).

Геометрические размеры червяка и колеса определяют по формулам, аналогичным формулам дня зубчатых колес.

В червячной передаче расчетным является осевой модуль червяка m_s, равный окружному модулю червячного колеса m_t.

Основными геометрическими размерами червячного зацепления являются (Рисунок 78):

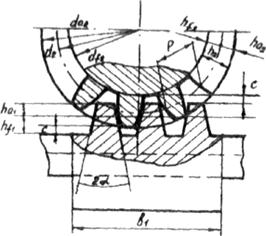
Рис 78.

1) Угол профиля зуба колеса 2α равен углу профиля витка червяка в осевом сечении ; 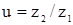- передаточное число;

2) Осевой шаг червяка - осевой модуль;

3) Ход винтовой линии (Рисунок 79),, z - число заходов червяка;

Рис 79.

4) Высота головки зуба ;

5) Высота ножки зуба , тогда боковой зазор ;

6) Коэффициент диаметра червяка (число модулей в диаметре делительного цилиндра) ;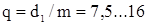

7) Делительные диаметры червяка 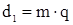; и колеса ;

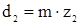8) Начальные диаметры червяка 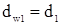; и колеса ;

9) Диаметры окружности выступов

,

;

10) Диаметры окружности впадин

,

;

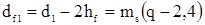11) Межосевое расстояние

;

12) Длина нарезной части червяка b₁ - в зависимости от числа заходов z₁: при . От z₁ зависит наружный диаметр колеса ; ширина – b₂ - колеса ;

13) Угол подъема винтовой линии червяка (Рисунок 79) - ход винтовой линии.

;

Рис 80.

14) Угол обхвата червяка колесом .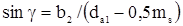

Во время работы червячной передачи нитки червяка скользят по зубьям червячного колеса.

Скорость скольжения V_ск направлена по касательной к винтовой линии делительного цилиндра червяка (Рисунок 80).

Векторы окружных скоростей червяка V₁ и колеса V₂ взаимно перпендикулярны (Рисунок 80).

,

.

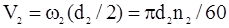Скорость скольжения определяется из параллелограмма скоростей

V_cк всегда больше V₁. Большое скольжение в червячной передаче повышает износ зубьев колеса, увеличивает склонность к заеданию.

3.8.3 Материалы червячной пары.

Материалы червячной пары должны иметь низкий коэффициент трения, обладать хорошей износостойкостью и пониженной склонностью к заеданию.

Червяки изготавливают из среднеуглеродистой стали 40,45,50 ГОСТ 1050-88, легированной стали 40Х, 40ХН, ЗОХГСА. Термообработка - закалка до 45-55 HRC с последующей шлифовкой.

Венцы колес: при V_ск = 6...25 м/с - оловянистые бронзы

БрОФЮ-1, БРОНФ, БрО1Ф1, БрО1ОН1Ф1. При V_ск = 2...6 м/с применяют алюминиевые бронзы Бр А9Ж-4, БрА10Ж4Н4, при V_cк<2 м/с применяют серый чугун СЧ12, СЧ15, ГОСТ 1412-85, σ_в =120 МПа и 150 МПа при растяжении.

3.8.4 Силы, действующие в зацеплении.

Показывают в двух плоскостях (Рисунок 81).

Рис 81.

Дата добавления: 2013-12-14