Decision making in critical Care

Пример 2. Процесс случайного блуждания. (Random walk).

Пример 1. Процесс et, который удовлетворяет условиям Гаусса-Маркова.

Примеры к лекциям 1, 2

Приведем несколько простейших примеров случайных процессов.

Это означает, что

.

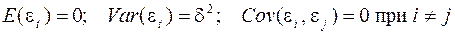Этот процесс заведомо стационарен в слабом или в широком смысле. Если добавить еще, что e нормальна, что он стационарен еще и в сильном смысле. Мы этот процесс будем называть белый шум (white noise), поэтому мы будем писать: . Этот процесс является стационарным. Он играет очень важную роль, порождает более сложные процессы.

Иногда его называют броуновским движением. Это процесс, который выражается следующим образом:

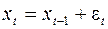. (1)

Это процесс авторегрессии с коэффициентом 1.

Сам термин «случайное блуждание» появился где-то в начале века в связи с исследованиями каких-то ученых. Они обсуждали задачу: если в чистом поле выпустить пьяного, то через некоторое время – где его следует искать? Один из результатов – надо искать на том же месте, потому у него случайного блуждания, то есть в среднем он останется на том же месте.

Давайте посмотрим, что мы можем сказать про этот процесс, про его математическое ожидание, дисперсию, ковариацию и так далее. Процесс (1) – это обычное разностное уравнение. Нам легко записать его решение:

.

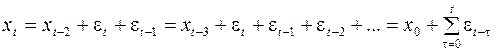Мы выписали решение в явном виде не через предыдущие значения, а только через правые части, в которых стоит белый шум. Запишем процесс иначе:

.

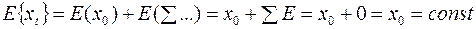То есть математическое ожидание удовлетворяет условию стационарности. Что можно сказать о дисперсии?

.

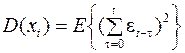Если мы раскроем скобки, то удвоенные произведения по свойствам белого шума уйдут в 0, а останутся только суммы квадратов. То есть:

.

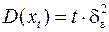Сомножитель t показывает, что дисперсия случайного блуждания меняется со временем, более того она растет пропорционально времени.

Наш процесс случайного блуждания является нестационарным, даже в широком смысле, так как дисперсия не постоянна, она меняется во времени.

Обратим внимание на следующую интересную особенность. Мы могли это же уравнение 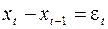переписать в виде . D можно рассмотреть как другой временной ряд, переобозначим через z_t, тогда z_t = e _t. Если мы возьмем первую разность нестационарного ряда, то в результате можем получить новый ряд, который будет стационарным. Это один из самых простых способов остационаривания ряда.

Мы уже интуитивно должны с вами чувствовать, что со стационарным рядом работать гораздо проще. Но возникает вопрос. А много ли таких стационарных рядов? Далеко не всегда наши экономические показатели ведут себя стационарно.

Оказывается, можно разделять наш исходный ряд на составляющие:

,

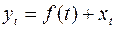где x_t – случайная часть, f (t) – детерминированная часть (т.е. эту составляющую можно точно предсказать наперед).

Давайте рассмотрим некоторые примеры, чтобы пояснить, что имеется в виду. Предположим, что случайный ряд имеет следующий вид

.

Мы уже рассматривали такие регрессии, это регрессия на время t. 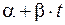– детерминированная часть.

Если все это изобразить на графике, то получим некоторый тренд, вокруг которого совершается некоторое движение:

Если e _t является стационарным процессом, то . Здесь математическое ожидание зависит от t, т.е. этот случайный процесс является не стационарным. Задача выделения тренда тоже входит в круг наших интересов.

Как описать стационарный процесс? Наше определение может быть еще позволяет определить: является ли наш процесс стационарным, но как написать общее выражение для стационарного процесса?

Пример 3. Процессы скользящего среднего (МА) [1]

Процесс описывается скользящем средним порядка q, если в нашем ряду только q слагаемых. То есть:

.

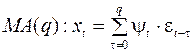Сейчас мы описываем просто абстрактную схему: что собой представляет ряд. Когда мы будем с ними уже работать, надо понимать, что, как и в эконометрике, e – ненаблюдаемая величина. Поэтому, договорились, что можно без потери общности отнормировать один коэффициент, то положить коэффициент при e _t, то есть когда t = 0, равным единице: 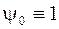– так договорились для упрощения записи. И тогда этот ряд можно представить в виде:

.

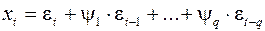Вот это и будет процесс скользящего среднего порядка q. Почему он так называется? Потому что мы вроде бы взяли текущее значение случайного возмущения, белого шума и сложили с некоторыми весами, то есть мы такое среднее взяли. Процедуру скользящего среднего часто используют для того, чтобы сгладить данные, которые сильно колеблются.

С войства этого ряда:

Процесс стационарен.

Математическое ожидание: .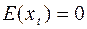

Дисперсия: .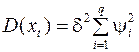

Итак, мы видим, что ни математическое ожидание, ни дисперсия не зависят от времени.

Ковариация: 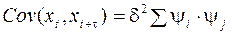.[2] В данном случае i и j связаны между собой. Эта формула не будет зависеть от t, она будет зависеть только от t. Самое интересное, что как только t > q, в этих выражениях нет ни одного совпадающего e.

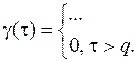[3]

[1] МА = moving average

[2] Необходимо вывести эту формулу самостоятельно.

[3] Попробуйте самостоятельно вывести, что будет, если t £ q.

HILLARY DON, M.D.

Associate Professor

Department of Anesthesia

Director, Intensive Care Unit

University of California School of Medicine San Francisco, California

B.C. DECKER INC. • Toronto • Philadelphia

THE C.V. MOSBY COMPANY • Saint Louis • Toronto • London

Дата добавления: 2013-12-14