Множественная линейная корреляция

При изучении сложных явлений необходимо учитывать более двух случайных факторов. Правильное представление о природе связи между этими факторами можно получить только в том случае, если подвергнуть исследованию сразу все рассматриваемые случайные факторы. Совместное изучение трех и более случайных факторов позволит исследователю установить более или менее обоснованные предположения о причинных зависимостях между изучаемыми явлениями. Простой формой множественной связи является ли­нейная зависимость между тремя признаками. Случайные факторы обозначаются как X ₁, X ₂ и X ₃. Парный коэффициенты корреляции между X ₁ и X ₂ обозначается как r ₁₂, соответственно между X ₁ и X ₃ - r ₁₂, между X ₂ и X ₃ - r ₂₃. В качестве меры тесноты линей­ной связи трех признаков используют множественные ко­эф-фициенты корреляции, обозначаемые R _1ּ23, R _2ּ13, R _3ּ12 и частные коэффициенты корреляции, обозначаемые r _12.3, r _13.2, r _23.1.

Множественный коэффициент корреляции R_1.23 трех факторов - это показатель тесноты линейной свя­зи между одним из факторов (индекс перед точкой) и совокупностью двух других факторов (индексы после точ­ки).

Значения коэффициента R всегда находятся в преде­лах от 0 до 1. При приближении R к единице степень линейной связи трех признаков увеличивается.

Между коэффициентом множественной корреляции, например R _2ּ13, и двумя коэффициентами парной корреляции r ₁₂ и r ₂₃ существует соот­ношение: каждый из парных коэффициентов не может превы­шать по абсолютной величине R _2ּ13.

Формулы для вычисления множественных коэффициентов корреляции при известных значениях коэффициен­тов парной корреляции r₁₂, r₁₃ и r₂₃ имеют вид:

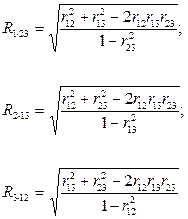
Квадрат коэффициента множественной корреляции R ² назы­вается коэффициентом множественной детерминации. Он пока­зывает долю вариации зависимой переменной под воздействием изучаемых факторов.

Значимость множественной корреляции оценивается по F -критерию:

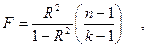
где

n – объем выборки; k – число факторов. В нашем случае k = 3.

Нулевая гипотеза о равенстве множественного коэффициента корреляции в совокупности нулю (H_o: R =0)принимается, если F _ф< F_t, и отвергается, если
F _ф ³ F _т .

Теоретическое значение F -критерия определяется для v ₁ = k - 1 и v ₂ = n - k степеней свободы и принятого уровня значимости a (при­ложение 1).

Пример вычисления коэффициента множественной корреляции. При изучении взаимосвязи между факторами были получены коэффициенты парной корреляции (n =15): r ₁₂==0,6; г₁₃ = 0,3; r ₂₃ = - 0,2.

Необходимо выяснить зависимость признака X ₂ от признака X ₁ и X ₃, т. е. рассчитать коэффициент множественной кор­реляции:

Табличное значение F -критерия при n₁ = 2 и n₂ = 15 – 3 = 12 степенях свободы при a = 0,05 F _0,05 = 3,89 и при a = 0,01 F _0,01 = 6,93.

Таким образом, взаимосвязь между признаками R _2.13 = 0,74 значима на
1%-ном уровне значимости F _ф > F _0,01.

Судя по коэффициенту множественной детерминации R ² = (0,74)² = 0,55, вариация признака X ₂ на 55% связана с действием изучаемых факторов, а 45% вариации (1-R²) не может быть объяснено влиянием этих переменных.

Дата добавления: 2013-12-14