Матричная игра

Основные определения

Лекция 2

основные понятия теории игр

Матричная игра

Теория игр это прикладная наука, предметом которой является математическое изучение конфликтных ситуаций, когда результат действия (решения) одной из сторон зависит от действий (решений) других сторон в условиях неполной статистической информации.

Игра это упрощенная формализованная модель конфликтной ситуации.

Для математического описания ситуации необходима ее формализация, которая состоит в том, что действия сторон подчиняются определенным правилам. Правила игры предопределяют возможные варианты действия сторон, объем информации каждой стороны о действиях других сторон, результат (исход) игры (выигрыш или проигрыш), который характеризуется числовым значением, при том или ином варианте действия сторон.

Парная игра это игра двух сторон (игроков) 1 и 2.

Игра с нулевой суммой это игра, в которой интересы игроков прямо противоположны (антагонистическая), а выигрыш одного из игроков равен проигрышу другого, и поэтому достаточно рассматривать только выигрыш игрока 1.

Стратегия игрока это правило действия игрока в каждой возможной ситуации игры.

В зависимости от числа возможных стратегий игроков различают конечные и бесконечные (непрерывные) игры.

Матричная игра это конечная игра с нулевой суммой.

Пусть в конечной игре с нулевой суммой игрок 1 имеет стратегии x ₁, x ₂,…, x_m, а игрок 2 имеет стратегии y ₁, y ₂,…, y_n. Такая игра называется игрой 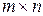. Выигрыш игрока 1 при стратегиях сторон x_i и y_j обозначим a_ij (если выигрыш является случайной величиной, то a_ij средний выигрыш или математическое ожидание выигрыша).

Все значения выигрышей составляют матрицу A =[ a_ij ], которая называется матрицей игры (матрицей эффективности или платежной матрицей).

	y 1	y 2	…	yn
x 1	a 11	a 12	…	a 1 n
x 2	a 21	a 22	…	a 2 n
…	…	…	…	…
xm	am 1	am 2	…	amn

Рассмотрим стратегии игрока 1. Выбирая стратегию x_i, игрок 1 должен принять, что игрок 2 ответит на нее такой стратегией y_j, которая дает игроку 1 минимальный выигрыш

(2.2.1)

Очевидно, игрок 1 должен выбрать ту из своих стратегий (строк матрицы), которой соответствует максимальное значение

(2.2.2)

Величину α называют нижней ценой игры или максимином, а соответствующую строку матрицы игры― максиминной стратегией. Максиминная стратегия игрока 1 обеспечивает ему выигрыш не меньший, чем α при любой стратегии игрока 2.

Если игрок 1 не информирован о действиях игрока 2, то есть не знает его конкретную стратегию y_j, то максиминная стратегия является оптимальной чистой гарантирующей стратегией игрока 1, а величина α ―максимальным гарантированным выигрышем для него.

Рассмотрим теперь стратегии игрока 2. Игрок 2, выбирая свою стратегию y_j, должен принять, что игрок 1 ответит на нее такой стратегией x_i, которая дает максимальный выигрыш

(2.2.3)

Очевидно, игрок 2 должен выбрать ту из своих стратегий (столбцов матрицы), которой соответствует минимальное значение

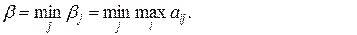(2.2.4)

Величину β называют верхней ценой игры или минимаксом, а соответствующий столбец матрицы игры― минимаксной стратегией. Минимаксная стратегия игрока 2 гарантирует ему проигрыш не больший, чем β при любой стратегии игрока 1.

Если игрок 2 не информирован о действиях игрока 1, то есть не знает его конкретную стратегию x_i, то минимаксная стратегия является оптимальной чистой гарантирующей стратегией игрока 2, а величина β ―минимальным гарантированным проигрышем для него.

Максиминная и минимаксная гарантирующие стратегии соответствуют осторожному подходу к решению задачи. Они выбираются в условиях, когда каждый из игроков не информирован о действиях другого, но предполагает, что противник знает его конкретную стратегию и действует наиболее неблагоприятным для него способом.

Дата добавления: 2013-12-13