Лекция 4. Пример решения матричной игры с седловой точкой

Пример решения матричной игры с седловой точкой.

Пример решения матричной игры в чистых стратегиях.

Лекция 3

Матричная игра (продолжение)

Пример 3.1 Определение нижней цены игры, верхней цены игры, максиминной и минимаксной стратегии для заданной матрицы игры

	y 1	y 2	y 3	y 4
x 1
x 2

Здесь α ₁ = 2, α ₂ = 3, α= 3, β ₁ = 8, β ₂ = 5, β ₃ = 8, β ₄ = 7, β= 5.

x ₂―максиминная стратегия, y ₂―минимаксная стратегия.

Таким образом, если игрок 1 не информирован о действиях игрока 2, то максимальным гарантированным выигрышем для него является α= 3 (нижняя цена игры), а вот если он информирован о действиях игрока 2, то тогда максимальным гарантированным выигрышем для него является минимальный гарантированный проигрыш игрока 2, то есть β= 5 (верхняя цена игры). В этом случае оптимальная стратегия игрока 1 определяется при нахождении максимума, а не максимина.

Можно показать, что в антагонистической игре .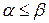

Если для данной игры нижняя и верхняя цены игры совпадают

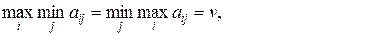(3.2.1)

то игрок 1 может выиграть v, но больше, чем v игрок 2 может не дать ему выиграть, поэтому v это чистая цена игры.

В этом случае матрица игры содержит элемент, который является минимальным в своей строке и максимальным в своем столбце. Этот элемент называется седловой точкой матрицы, соответствующие ему стратегии называются ситуацией равновесия, а сама игра при этом называется игрой с седловой точкой, игрой с ситуацией равновесия или вполне определенной игрой.

Чистые максиминная и минимаксная стратегии вигре с седловой точкой являются оптимальными независимо от информированности игроков.

Если игрок 2 придерживается своей минимаксной стратегии, то игроку 1 не выгодно отклоняться от своей максиминной стратегии и наоборот.

Можно показать, что оптимальность поведения игроков не изменится, если матрица игры умножается на положительную константу или к ней прибавляется константа.

Пример 3.2 Определение чистой цены игры, максиминной и минимаксной стратегии для заданной матрицы игры с седловой точкой

	y 1	y 2	y 3
x 1
x 2
x 3

Здесь α ₁ = 2, α ₂ = 5, α ₃ = 3, α= 5, β ₁ = 7, β ₂ = 6, β ₃ = 5, β= 5, v= 5, a ₂₃ = 5―седловая точка, x ₂―максиминная стратегия, y ₃―минимаксная стратегия, (x ₂, y ₃)―ситуация равновесия.

Максиминная x ₂ и минимаксная y ₃ стратегии являются оптимальными независимо от информированности игроков. Так, если игрок 2 придерживается минимаксной стратегии y ₃ игроку 1 не выгодно отклоняться от своей максиминной стратегии x ₂ даже при условии информированности, а вот в игре без седловой точки при информированности игрока 1 его оптимальная стратегия не совпадала с максиминной.

смешанное расширение Матричной игры

Дата добавления: 2013-12-13