Решение матричной игры

Лекция 5

методы решения Матричных игр

в смешанных стратегиях

Решением игры называют также нахождение оптимальных смешанных стратегий и цены игры.

Рассмотрим простейшую игру 2×2.

	y 1	y 2
x 1	a 11	a 12
x 2	a 21	a 22

Здесь возможны 2 варианта.

Если игра имеет седловую точку, то решение игры―две чистые стратегии (максиминная для игрока 1 иминимаксная для игрока 2), которые ее содержат.

Если игра не имеет седловой точки, то решение игры―две оптимальные смешанные стратеги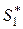и и .

Найдем оптимальную смешанную стратегию игрока 1

(5.1.1)

Поскольку обе стратегии игрока 2 являются активными (в противном случае игрок 2 пользовался бы только одной минимаксной чистой стратегией, что соответствует игре с седловой точкой), то на основании свойства оптимальных смешанных стратегий получим уравнения (средний выигрыш остается неизменным и равным цене игры γ независимо от того, какой смесью активных стратегий или какой одной чистой стратегией пользуется другой игрок)

(5.1.2)

Отсюда

(5.1.3)

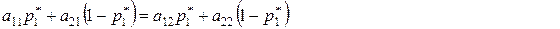(5.1.4)

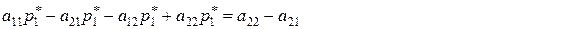(5.1.5)

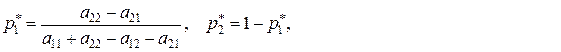(5.1.6)

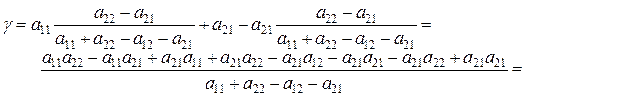
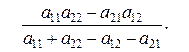(5.1.7)

Найдем теперь оптимальную смешанную стратегию игрока 2

(5.1.8)

Для этого достаточно уравнений

(5.1.9)

Отсюда

(5.1.10)

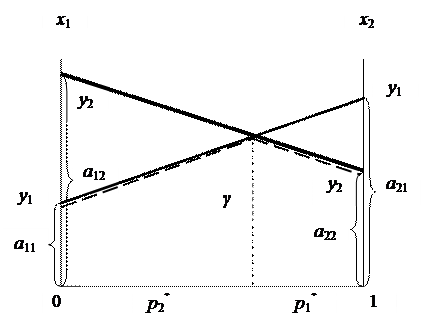
Решению игры 2×2можно дать геометрическую интерпретацию. Средний выигрыш игрока 1 при стратегии y ₁ равен 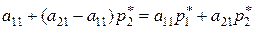. Нижняя граница выигрыша показана пунктиром, ее максимум ― цена игры и ее

решение.

Дата добавления: 2013-12-13