Применение линейного программирования

Лекция 6

методы решения Матричных игр

в смешанных стратегиях (продолжение)

В общем случае решение игры m × n сводится к задаче линейного программирования (при 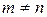система линейных уравнений не имеет решения или имеет бесконечное множество решений).

Пусть цена игры с матрицей 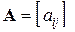положительна 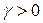(этого всегда можно добиться, прибавляя к каждому элементу матрицы одну и ту же достаточно большую положительную величину, что не меняет решения игры).

Средний выигрыш игрока 1 при его оптимальной смешанной стратегии 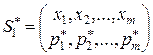и любой чистой стратегии 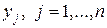игрока 2 остается неизменным и равным цене игры γ

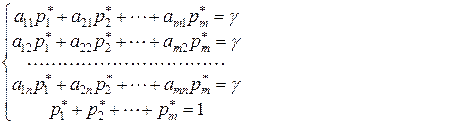(6.1.1)

Поскольку при m ≠ n решение системы неоднородных линейных уравнений (6.1.1) найти невозможно, перейдем к эквивалентной (вспомогательной) задаче линейного программирования, учитывая, что средний выигрыш, равный цене игры, мы хотим сделать максимально возможным, а также то, что , .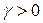

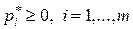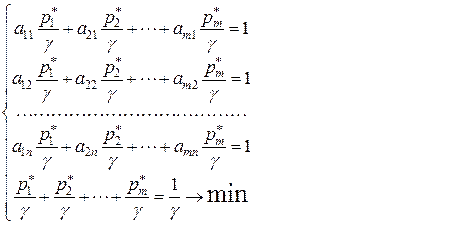(6.1.2)

Обозначив 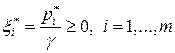, получим

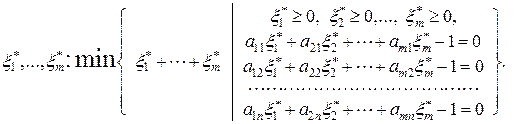(6.1.3)

Здесь можно при необходимости заменить ограничения в виде равенств парами ограничений в виде неравенств.

Аналогично, средний проигрыш игрока 2 при его оптимальной смешанной стратегии 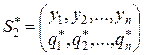и любой чистой стратегии 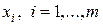игрока 1 остается неизменным и равным цене игры γ

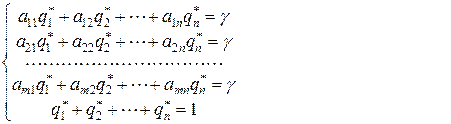(6.1.4)

Далее перейдем к эквивалентной задаче линейного программирования, учитывая, что средний проигрыш, равный цене игры, мы хотим сделать минимально возможным, а также то, что , .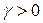

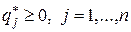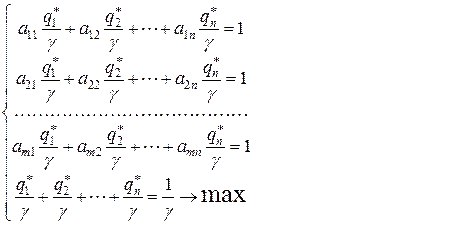(6.1.5)

Обозначив 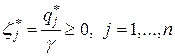, получим

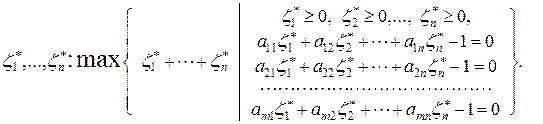(6.1.6)

Здесь также можно заменить ограничения в виде равенств парами ограничений в виде неравенств.

С другой стороны, средний выигрыш игрока 1 при его оптимальной смешанной стратегии 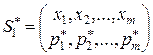и любой чистой стратегии 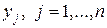игрока 2 в силу (3.2.2) будет не меньше, чем цена игры γ

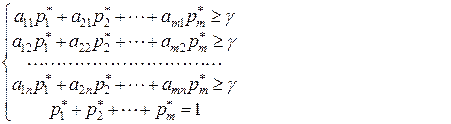(6.1.7)

Соответственно, вспомогательная задача линейного программирования может быть записана в виде

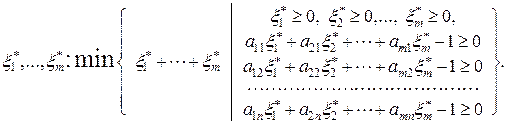(6.1.8)

Аналогично, средний проигрыш игрока 2 при его оптимальной смешанной стратегии 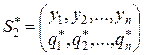и любой чистой стратегии 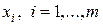игрока 1 в силу (3.2.2) будет не больше, чем цена игры γ

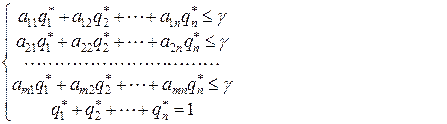(6.1.9)

Соответственно, вспомогательная задача линейного программирования

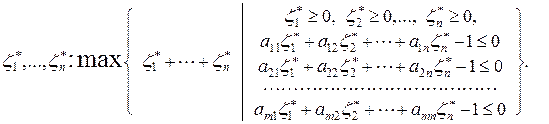(6.1.10)

Задачи (4.2.8) и (4.2.10) это прямая и двойственная задачи линейного программирования.

Пример 6.1 Решение игры с помощью линейного программирования

	y 1	y 2
x 1
x 2

Здесь α ₁ = 0, α ₂ = 2, α= 2, β ₁ = 4, β ₂ = 3, β= 3, x ₂―максиминная стратегия, y ₂―минимаксная стратегия, седловая точка и ситуация равновесия отсутствуют.

Вначале найдем точное решение игры для игрока 1 и игрока 2 с помощью решения систем линейных уравнений вида (6.1.1) и (6.1.4).

Система

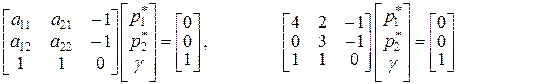
имеет решение, состоящее из положительных величин

Система

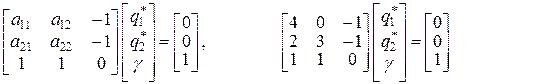
тоже имеет решение, состоящее из положительных величин

Соответствующие задачи линейного программирования имеют вид

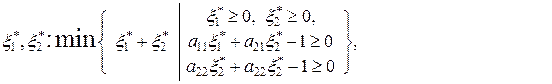
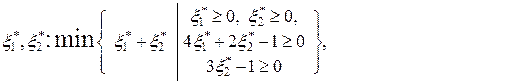
и

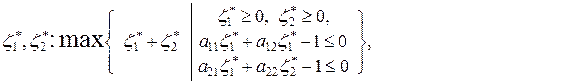
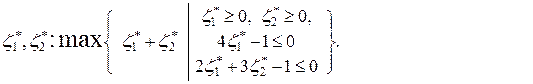
Решение игры можно найти графически.

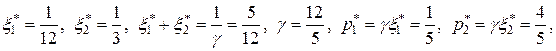
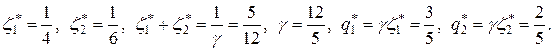
Дата добавления: 2013-12-13