Метод решения бесконечных игр

Пример решения игры методом Брауна-Робинсона

Лекция 8

итерационный метод решения Матричной игры

(продолжение)

Пример 8.1 Решение игры итерационным методом

	y 1	y 2	y 3
x 1
x 2
x 3

Вначале найдем точное решение игры для игрока 1 с помощью решения системы линейных уравнений вида (6.1.1).

Система

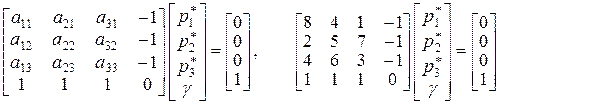
имеет решение, состоящее из положительных величин

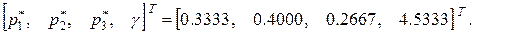
Построим таблицу итерационного процесса для данного примера.

k	ik	kμ 1	kμ 2	kμ 3	jk	kη 1	kη 2	kη 3	γ 1	min γ 1	γ 2	max γ 2	Δ
		1 30 34 38 50 80 81 85 89 97	11 16 21 26 45 52 54 59 64 69 76 104 106 111	7		8 12 44 54 56 98 104 106	15 20 25 34 38 47 61 66 71 89 93 111 116	32 78 85 86	5.33 4.86 4.75 4.89 4.7 4.91 4.67 4.69 4.71 4.73 4.88 4.78 4.68 4.65 4.67 4.72 4.61 4.63 4.64	4.86 4.75 4.75 4.7 4.7 4.67 4.67 4.67 4.67 4.67 4.67 4.67 4.67 4.65 4.65 4.65 4.61 4.61 4.61	3.5 3.67 4.2 4.33 4.29 4.25 4.23 4.5 4.55 4.33 4.15 4.21 4.27 4.31 4.47 4.44 4.26 4.25 4.24 4.41 4.52 4.42 4.44	3.5 3.67 4.2 4.33 4.33 4.33 4.33 4.5 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55 4.55	2.5 1.33 0.8 0.67 0.53 0.42 0.42 0.2 0.15 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.12 0.1 0.1 0.1 0.06 0.06 0.06

Получаем .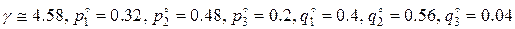

Бесконечной игрой называется игра, в которой по крайней мере одна из сторон имеет бесконечное множество стратегий.

Рассмотрим игру двух противников 1 и 2, каждый из которых имеет бесконечное и несчетное множество стратегий. Для игрока 1 эти стратегии соответствуют различным значениям переменной x, а для игрока 2 ― различным значениям переменной y. Вместо матрицы игры [ a_ij ] здесь используется функция выигрыша a (x, y).

Нижняя цена игры

(8.2.1)

а верхняя цена игры

(8.2.2)

Если α=β, тофункция выигрыша a (x, y) имеет седловую точку, а игра имеет решение в области чистых стратегий, которые представляют собой координаты этой точки. В противном случае игра может иметь решение в области смешанных стратегий, которые представляют собой распределение вероятностей для случайных величин x и y. Эти распределения могут быть непрерывными p (x) и q (y) или дискретными.

Одним из практических способов решения бесконечных игр является их приближенное сведение к конечным. При этом конечно возможны не только погрешности, но и ошибки, например, может быть найдено решение в области смешанных стратегий для игры, имеющей седловую точку (в этом случае две активные стратегии, которые только и входят в оптимальную смешанную стратегию, являются соседними).

Дата добавления: 2013-12-13