Биматричная игра

Лекция 9

неантагонистические игры двух игроков

Бескоалиционной неантагонистической игрой двух игроков (1 и 2)называется игра, в которой игроки одновременно и независимо друг от друга выбирают свои стратегии, и выигрыш каждого из игроков в каждой ситуации игры определяется его собственнойфункцией выигрыша или матрицей игры.

Конечная бескоалиционная игра двух игроков называется биматричной (матрицы игры двух игроков A и B). Биматричную игру можно также задать матрицей (A, B), элементы которой представляют собой пары чисел (a_ij, b_ij), i= 1,…, m, j= 1,…, n.

Пример 9.1 Биматричная игра («семейный спор»)

	y 1	y 2
x 1	(4, 1)	(0, 0)
x 2	(0, 0)	(1, 4)

Игрок 1 («муж») и игрок 2 («жена») могут выбрать одно из двух вечерних развлечений: футбол (4, 1) или театр (1, 4). Игрок 1 («муж») предпочитает футбол, а игрок 2 («жена») — театр. Если их намерения не совпадают, то они остаются дома (0, 0) или (0, 0). При этом каждому из них предпочтительнее провести время вместе вне дома.

В антагонистической игре каждому из игроков невыгодно информировать своего противника о стратегии, которую он собирается применить. В неантагонистической игре каждому из игроков выгодно первому объявить о своей стратегии и договариваться о совместных действиях, иначе они оба могут проиграть.

В антагонистической игре ситуация равновесия (седловая точка, если она существует) совпадает с решением игры в чистых стратегиях (с точкой максимина и минимакса). В неантагонистических играх существует несколько различных подходов к определению ситуаций равновесия и к определению оптимальности поведения.

Для биматричной игры ситуация (x_k, y_l) называется ситуацией равновесия по Нэшу, если

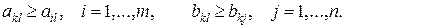(9.1.1)

В примере 9.1 равновесными являются ситуации (x ₁, y ₁) и (x ₂, y ₂).

Важная особенность ситуации равновесия по Нэшу в биматричной игре заключается в том, что отклонение от нее двух игроков может привести к увеличению выигрыша одного из них или обоих.

Коалиция это некоторое подмножество множества игроков.

Для биматричной игры ситуация (x_k, y_l) называется сильно равновесной, если для любых коалиций

(9.1.2)

Это условие гарантирует нецелесообразность соглашения между игроками о вступлении в коалицию, так как в любой коалиции одного из игроков это соглашение не устраивает.

Любая сильно равновесная ситуация является равновесной.

В примере 9.1 равновесные ситуации (x ₁, y ₁) и (x ₂, y ₂) являются сильно равновесными.

Пример 9.2

	y 1	y 2
x 1	(5, 5)	(0, 10)
x 2	(10, 0)	(1, 1)

Здесь одна ситуация равновесия по Нэшу (x ₂, y ₂) (не сильно равновесная) дает игрокам выигрыши (1, 1). Однако если оба игрока сыграют (x ₁, y ₁), то они получат выигрыши (5, 5). Таким образом, ситуация (x ₁, y ₁) не является равновесной, но она лучшая для обоих игроков. При этом сильно равновесной ситуации в этой игре нет.

Ситуация (x_k, y_l) в биматричной игре называется ситуацией оптимальной по Парето, если не существует ситуации (x_r, y_s), для которой имеют место неравенства

(9.1.3)

и

(9.1.4)

или

(9.1.5)

Оптимальность ситуации (x_k, y_l) по Парето означает, что не существует ситуации (x_r, y_s), которая была бы предпочтительнее ситуации (x_k, y_l) для всех игроков. В ситуации равновесия по Нэшу ни один игрок, действуя в одиночку, не может увеличить своего выигрыша, а в ситуации оптимальной по Парето все игроки, действуя совместно, не могут (даже не строго) увеличить выигрыш каждого.

Сильно равновесная ситуация являетсяоптимальной по Парето.

В примере 9.2 ситуация (x ₂, y ₂) является равновесной, но не является оптимальной по Парето, а ситуация (x ₁, y ₁), наоборот, оптимальна по Парето, но не является равновесной.

В примере 9.1 обе равновесные ситуации (x ₁, y ₁) и (x ₂, y ₂) являются сильно равновесными и оптимальными по Парето.

Если биматричная игра имеет две оптимальных по Парето равновесных по Нэшу ситуации, то в ней имеет место борьба за лидерство.

Лидер это игрок, который знает обе матрицы игры, а значит и наилучшие ответы противника. В этом случае он максимизирует свой выигрыш в ситуации, которая называется i- равновесием по Штакельбергу (i- ый игрок действует оптимально в качестве лидера).

Дата добавления: 2013-12-13