Лекция 10. 10.1. Бескоалиционная игра n игроков

неантагонистические игры n игроков

10.1. Бескоалиционная игра n игроков

Бескоалиционной неантагонистической игрой n игроков (1, 2,…, n)называется игра, в которой игроки одновременно и независимо друг от друга выбирают свои стратегии ⁱx, i =1, 2,…, n, в результате чего формируется ситуация (¹ x, ² x,…, ⁿx), после чего каждый игрок получает выигрыш ⁱa (¹ x, ² x,…, ⁿx), i =1, 2,…, n.

Ситуация (¹ x ^*, ² x ^*,…, ⁿx ^*) называется ситуацией равновесия по Нэшу, если

(10.1.1)

Отклонение от ситуации равновесия по Нэшу двух и более игроков может привести к увеличению выигрыша одного из них.

Ситуация (¹ x ^*, ² x ^*,…, ⁿx ^*) называется сильно равновесной, если для любой коалиции игроков i ₁, i ₂,…, i_s

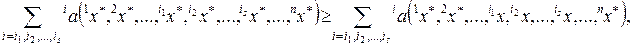
(10.1.2)

Это условие гарантирует нецелесообразность соглашения между игроками о вступлении в коалицию, так как в любой коалиции одного из игроков это соглашение не устраивает.

Ситуация (¹ x^p, ² x^p,…, ⁿx^p) называется ситуацией оптимальной по Парето, если не существует ситуации (¹ x, ² x,…, ⁿx), для которой имеют место неравенства

(10.1.3)

и хотя бы для одного j

(10.1.4)

10.2. Кооперативная игра n игроков

Кооперативной игрой n игроков (1, 2,…, n)называется игра, условия которой допускают совместные действия игроков и перераспределение выигрыша.

Представляется, что объединение игроков в максимальную коалицию (в коалицию, состоящую из всех игроков) при определенных условиях является целесообразным, то есть позволяет не только получить максимальный суммарный выигрыш, но и распределить его между членами коалиции таким образом, чтобы у них не возникало желание создавать меньшие коалиции или действовать индивидуально.

Пусть N= {1, 2,…, n } множество всех игроков. Любое непустое подмножество этого множества S= { i ₁, i ₂,…, i_s } называется коалицией s=|S| игроков.

Характеристической функцией игры n игроков называется вещественная функция u, определенная на коалициях 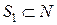, ,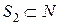…, , 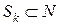при этом u (Ø)=0 и для любых непересекающихся коалици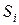й и 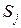выполняется неравенство

(10.2.1)

а, следовательно,

(10.2.2)

Таким образом, можно интерпретироватьхарактеристическую функцию коалиции как ее гарантированный выигрыш, когда она действует независимо от других игроков. При этом коалиция 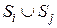имеет не меньше возможностей, чем две непересекающиеся коалици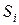и и 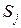, действующие независимо (свойство супераддитивности характеристической функции), и не существует такого разбиения множества N на коалиции, чтобы их суммарный выигрыш превышал выигрыш всех игроков u(N).

Как определить характеристическую функцию коалиции или ее гарантированный выигрыш? Суммарный выигрыш игроков, входящих в коалицию S

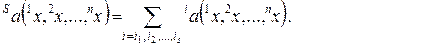(10.2.3)

В лучшем случае характеристическая функция коалиции равна суммарному выигрышу ее игроков, а в худшем случае все остальные игроки из N \ S объединены в коалицию с суммарным проигрышем 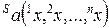. Тогда можно условно считать эти две коалиции двумя игроками, участвующими в антагонистической игре (размерности множеств стратегий этих двух игроков равны произведениям размерностей множеств стратегий игроков, входящих в соответствующие коалиции), цена которой в смешанных стратегиях (нижняя или чистая цена в чистых стратегиях) равна гарантированному суммарному выигрышу коалиции S.

Дата добавления: 2013-12-13