Смешанное расширение биматричной игры

Если определить смешанные стратегии игроков 1 и 2 для биматричной игры с помощью (4.1.1, 4.1.2) с учетом (4.1.3, 4.1.4), то мы получим смешанное расширение биматричной игры.

Средние выигрыши игроков 1 и 2 (математические ожидания результатов) при использовании смешанных стратегий

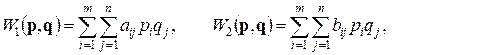(9.2.1)

где 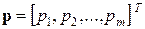, 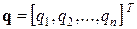векторы вероятностей использования чистых стратегий.

Для биматричной игры cмешанные стратеги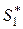и и образуют ситуацию равновесия по Нэшу в смешанных стратегиях, если

(9.2.2) (9.2.3)

Равновесные выигрыши игроков

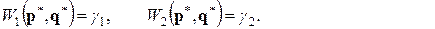(9.2.4)

Можно доказать существованиеситуации равновесия по Нэшу в смешанных стратегиях в любой биматричной игре.

Для того, чтобы в биматричной игреситуацияв смешанных стратегиях 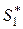и была ситуацией равновесия, необходимо и достаточно, чтобы для всех чистых стратегий, соответственно, игроков 1 и 2 выполнялись условия

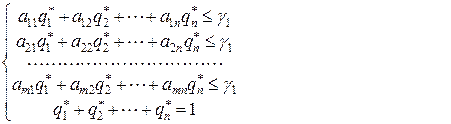(9.2.5)

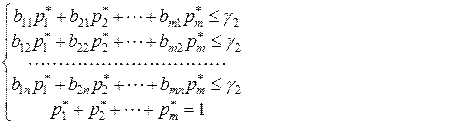(9.2.6)

В данном случае вспомогательные задачи линейного программирования

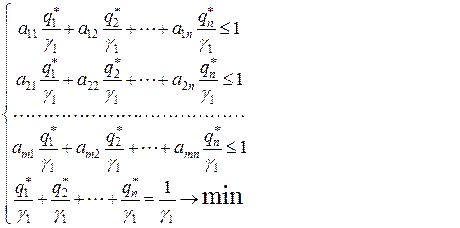(9.2.7)

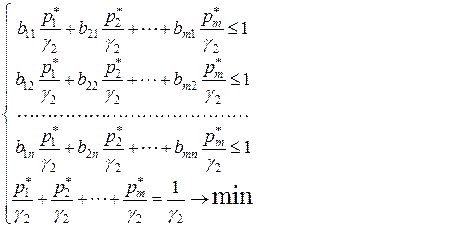(9.2.8)

С другой стороны, средний выигрыш игрока 1 остается неизменным и равным равновесному выигрышу γ ₁ при равновесной смешанной стратегии 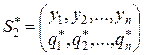игрока 2 и любой чистой стратегии 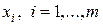игрока 1

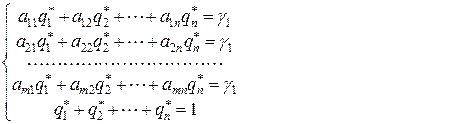(9.2.9)

Средний выигрыш игрока 2 остается неизменным и равным равновесному выигрышу γ ₂ при равновесной смешанной стратегии 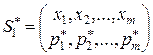игрока 1 и любой чистой стратегии 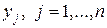игрока 2

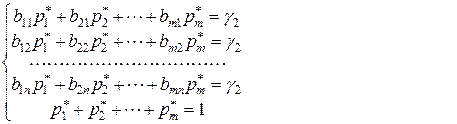(9.2.10)

Отсюда для примера 9.1 получим две системы линейных уравнений.

Система

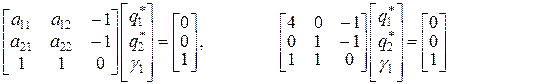
имеет решение, состоящее из положительных величин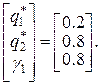

Система

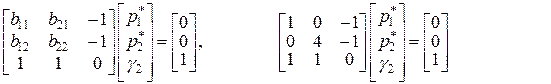
тоже имеет решение, состоящее из положительных величин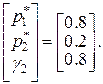

Соответствующие (9.2.7), (9.2.8) (9.2.9), (9.2.10) вспомогательные задачи линейного программирования имеют вид

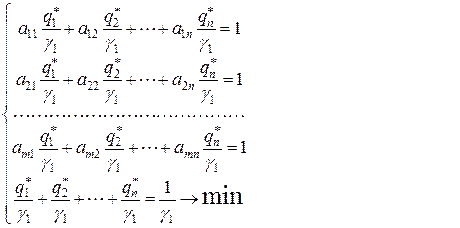(9.2.11)

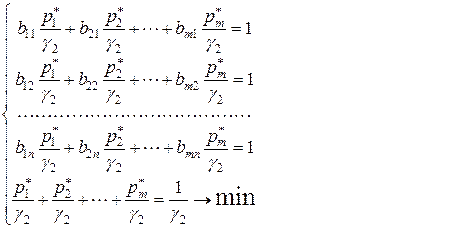(9.2.12)

Отсюда для примера 9.1 получим

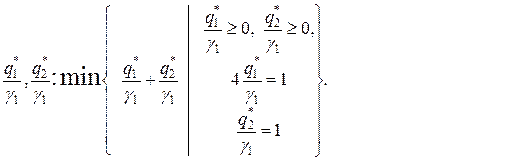
Решение

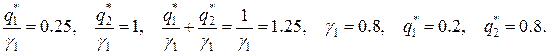
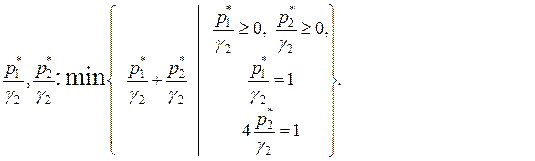
Решение

Соответствующие (9.2.7), (9.2.8) вспомогательные задачи линейного программирования не позволяют найти решение смешанного расширения биматричной игры.

Заметим, что смешанная равновесная ситуация по Нэшу с выигрышами γ ₁=0.8 и γ ₂=0.8 менее предпочтительна для игроков, чем каждая из ситуаций равновесия в чистых стратегиях. Если игра повторяется многократно, то игрокам имеет смысл сделать совместный выбор: с вероятностью 0.5 выбирать совместно ситуации (x ₁, y ₁) или (x ₂, y ₂). Тогда средний ожидаемый выигрыш игроков будет, очевидно, 2.5 и 2.5.

Дата добавления: 2013-12-13