Спецификация модели

В эконометрике широко используются статистические методы. Ставя цель дать количественное описание взаимосвязей между экономическими переменными, эконометрика прежде всего связана с методами регрессии и корреляции.

В зависимости от количества факторов, включенных в уравнение регрессии, принято различать простую (парную) и множественную регрессию.

Простая регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной y рассматривается как функция одной независимой (объясняющей) переменной x, т.е. это модель вида .

Множественная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной y рассматривается как функция нескольких независимых (объясняющих) переменных т.е. это модель вида .

Любое эконометрическое исследование начинается со спецификации модели, т.е. с формулировки вида модели, исходя из теории связи между переменными.

В первую очередь необходимо выделить из всех факторов, влияющих на рассматриваемый признак наиболее существенно влияющие факторы:

Парная регрессия достаточна, если имеется доминирующий фактор, который используют в качестве объясняющей переменной. Например, выдвигается гипотеза о том, что величина спроса у на товар А находится в обратной зависимости от цены Х; т.е.: 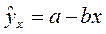. В этом случае нужно знать, какие факторы останутся неизменными; возможно в дальнейшем их придется учесть и от простой перейти к множественной. Т.е. связь между двумя переменными проявляется как некоторая закономерность лишь в среднем по совокупности наблюдений.

Практически в каждом отдельном случае величина y складывается из двух слагаемых: ,

Где 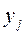- фактическое значение результативного признака;

- теоретическое значение результативного признака, найденное исходя из соответствующей математической функции связи y и x, т.е. из уравнения регрессии;

- случайная величина, характеризующая отклонение реального значения результативного признака от теоретического.

Случайная величина или возмущение включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения, ее присутствие обусловлено тремя источниками:

1) спецификация модели;

2) выборочным характером исходных данных;

3) особенностями измерения переменной.

От правильно выбранной спецификации модели зависит величина случайных ошибок: они тем меньше, чем в большей мере теоретические значения результативного признака подходят к фактическим данным y.

К ошибкам спецификации относят не только неправильный выбор математической функции , но и недоучет какого-либо существенного фактора (т.е. использование парной регрессии вместо множественной). Так спрос может определятся и ценой и доходом на душу населения.

Наряду с ошибками спецификации, могут быть ошибки выборки, поскольку исследователь чаще всего работает с выборочными данными при установлении закономерности. Ошибки выборки имеют место и в силу неоднородности данных в исходной совокупности. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Аномальные результаты обычно исключают из совокупности.

Наибольшую опасность представляют ошибки измерения. Если ошибки спецификации можно уменьшить, изменяя форму модели(вид математической формулы), а ошибки выборки – увеличивая объем исходных данных, то ошибки измерения сводят на нет все усилия количественной оценки связи. Например, органы статистики получают балансы предприятий, достоверность которых никто не подтверждает. Используя, например, в качестве результативного признака прибыль предприятия – мы должны быть уверены, что предприятие показывает реальные величины.

Предполагая, что ошибки измерения сведены к минимуму, основное внимание уделяется ошибкам спецификации.

В парной регрессии спецификация модели связана с выбором вида математической функции, а во множественной – также и с отбором факторов.

При построении могут быть использованы линейные () и нелинейные (например, .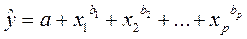

В большинстве стандартных прикладных программ предусмотрена процедура преобразования нелинейных функций в линейные.

В парной регрессии выбор вида математической функции может быть осуществлен тремя методами: графическим, аналитическим и экспериментальным.

Класс математических функций для описания достаточно широк. Основные типы:

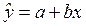
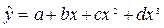
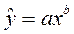
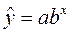
Дата добавления: 2013-12-14