
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статическая неопределимость внутренним образом
|
|
|
|
Статическая неопределимость.
Статически неопределимые системы.
Глава 11.
Статически неопределимой называется система, в которой число неизвестных (опорные реакции, реакции связи) больше основных уравнений равновесия.
Связи, накладываемые на систему сверх основных связей равновесия, называются дополнительными. Они определяются из дополнительных уравнений совместности деформаций. Число этих уравнений равно числу статической неопределимости системы.
Статическая неопределимость внешним образом:
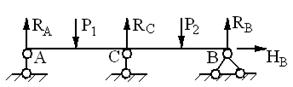
Система 1 раз статически неопределима.
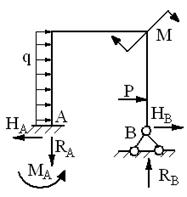
5 неизв.-3 уравнения равновесия=2 раза статически неопределима.
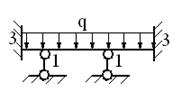
5 раз статически неопределима.
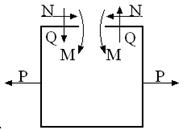
3 раза статически неопределим любой замкнутый контур независимо от формы.
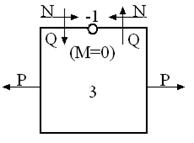
Система 2 раза статически неопределима.

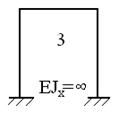
Система 3 раза статически неопределима.
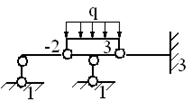
Плоский шарнир снимает (п-1) степеней статической неопределимости при сходящихся в нем п-стержней.
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 629; Нарушение авторских прав?; Мы поможем в написании вашей работы!