
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Структура системы управления
|
|
|
|
Таблица эквивалентных бесконечно малых
Лекция 22. Замечательные пределы. Первый и второй замечательные пределы. Таблица эквивалентных бесконечно малых.
Тема: Бюджетный процесс в Российской Федерации
Таблица 2 - Различия в деятельности предприятий с маркетинговой и производственной организационными культурами
Таблица 1 Определения маркетинга
Для студентов 1 курса 1 семестра
Лекция 1. Введение в курс. Элементы логики. Высказывания и предикаты, операции над ними. Кванторы. Построение отрицания сложного высказывания. Теорема как импликация. Прямая, обратная и противоположная теоремы, связь между ними. Доказательство от противного. Метод математической индукции. Бином Ньютона. Неравенство Бернулли. (25)
Лекция 2. Множества, операции над ними, их свойства. Множество действительных чисел, его полнота. Промежутки. Окрестности конечной точки и бесконечности. Принцип вложен-ных отрезков. Ограниченные и неограниченные множества. Точная верхняя и нижняя грани множества. (20)
Лекция 3. Функция (отображение), её график, аргумент и значение функции, область определения, множество значений, образ и прообраз. Сумма, произведение и композиция функций. Обратные функции. Свойства числовых функций (монотонность, ограниченность, чётность, периодичность). Класс элементарных функций. Примеры функций, не являющихся элементарными. (25)
Лекция 4. Числовая последовательность и её предел. Основные свойства пределов последовательностей (предел постоянной, единственность предела). Арифметические операции над сходящимися последовательностями. Ограниченность сходящейся последо-вательности. Признаки сходимости последовательностей. Критерий Коши, фундаментальная последовательность. Сходимость ограниченной монотонной последовательности. Число e. (20)
Лекция 5. Гиперболические функции, их свойства и графики. Два определения предела функции в точке (предел по Коши и предел по Гейне). Теорема об эквивалентности этих определений. Геометрическая иллюстрация предела. Предел функции в бесконечности. Бесконечные пределы. Единственность предела функции. Локальная ограниченность функции, имеющей конечный предел. Теорема о сохранении функцией знака своего предела. Предельный переход в неравенстве. Теорема о пределе промежуточной функции. (15)
Лекция 6. Односторонние пределы. Теорема о замене переменной в пределе (о пределе сложной функции). Арифметические операции с функциями, имеющими пределы. Первый и второй замечательные пределы. Следствия из них. (15)
Лекция 7. Бесконечно малые функции. Связь функции, ее предела и бесконечно малой. Свойства бесконечно малых функций. Бесконечно большие функции, их связь с бесконечно малыми. (15)
Лекция 8. Сравнение функций при данном стремлении аргумента. Эквивалентные бесконечно малые и бесконечно большие функции. Теоремы об эквивалентных функциях. Таблица эквивалентных бесконечно малых функций и её применение к вычислению пределов. Относительный порядок малости (или роста) функции при данном стремлении, выделение ее главной части. Теорема о сумме бесконечно малых разных порядков. (15)
Лекция 9. Непрерывность функции в точке: равносильные определения. Непрерывность суммы, произведения, композиции непрерывных функций. Свойства функций, непрерывных в точке. Односторонняя непрерывность функции. Непрерывность функции на промежутке (на интервале, полуинтервале и отрезке). Непрерывность основных элементарных функций (доказательство для многочлена и синуса). Точки разрыва функций, их классификация. (15)
Лекция 10. Свойства функций, непрерывных на отрезке: ограниченность, существование наибольшего и наименьшего значений, прохождение через любое промежуточное значение. Теорема о непрерывности обратной функции. Асимптоты графика функции. (15)
Лекция 11. Производная функции в точке, ее геометрический и механический смысл. Уравнения касательной и нормали к графику функции в заданной точке. Бесконечная производная, односторонние производные и их геометрический смысл. Дифференцируемость функции в точке, эквивалентность дифференцируемости существованию в точке конечной производной. Связь непрерывности и дифференцируемости. Основные правила дифферен-цирования функций. Дифференцирование обратных функций. (25)
Лекция 12. Таблица производных элементарных функций. Логарифмическая производная и ее применение. Производные высших порядков. Механический смысл второй производной. Дифференциал функции, его геометрический смысл. Правила вычисления дифференциалов. Инвариантность формы первого дифференциала. Применение дифференциалов к приближен-ным вычислениям. Дифференциалы высших порядков. Дифференцирование неявно и параметрически заданных функций (первая и вторая производная). (40)
Лекция 13. Основные теоремы дифференциального исчисления: Ферма, Ролля, Лагранжа и Коши. Теорема Бернулли - Лопиталя и раскрытие неопределенностей (доказательство только для [0/0]). Сравнение роста показательной, степенной и логарифмической функций в бесконечности. (25)
Лекция 14. Формула Тейлора с остаточным членом в форме Лагранжа и Пеано. Формула Маклорена и представление по этой формуле некоторых элементарных функций. Использо-вание формулы Тейлора в приближенных вычислениях и для вычисления пределов. (25)
Лекции 15. Необходимое и достаточное условия монотонности дифференцируемой функции на промежутке. Экстремум функции. Необходимое условие экстремума. Стационарные и критические точки функции. Достаточные условия экстремума (по первой и второй производным, по производной высшего порядка). Выпуклость (вверх и вниз) функции, точки перегиба. Достаточные условия выпуклости дважды дифференцируемой функции. Необходимые и достаточные условия наличия точки перегиба. (30)
Лекции 16. Схема полного исследования функции и построения ее графика. (35)
| Автор | Содержание |
| Котлер Ф. | Маркетинг— вид человеческой деятельности, направленной на удовлетворение нужд и потребностей посредством обмена |
| Абрамишвили Г. Г. | Сегодня маркетинг — это своеобразная философия ведения деловых операций |
| Браверман А. А. | На макроуровне маркетинг выступает в роли инструмента формирования рыночной среды. На микроуровне маркетинг выступает как инструмент встраивания предприятий в формируемую рыночную среду и, что особенно важно, является средством (часто решающим), обеспечивающим привлечение инвестиций |
| Американская ассоциация маркетинга | Маркетинг — представляет собой процесс планирования и осуществления замысла, ценообразование, продвижение и реализацию идей, товаров и услуг посредством обмена, удовлетворяющего цели отдельных лиц и организаций |
| Эванс Дж. Р. | Маркетинг — это предвидение, управление и удовлетворение спроса на товары, услуги, организации, людей, территории и идеи посредством обмена |
| Пашкус Ю. В. | Маркетинг — понятие комплексное. Оно включает в себя все виды деятельности, связанные с обменом между людьми или странами, направленные на удовлетворение потребностей и желаний потребителей |
| Швальбе X. | Маркетинг — это сумма всех действий в рамках политики товарооборота с целью создания, поддержания и расширения рынка |
| Нишлаг Р., Дихтль Е., Херштен X. | Маркетинг — это последовательная ориентация всех прямо или косвенно связанных с рынком решений на потребности покупателей. Маркетинг сегодня понимается как ориентированный на рынок предпринимательский стиль мышления, который отличается творческим, систематическим и иногда также агрессивным характером |
| Ламбен Ж.-Ж. | Маркетинг — это одновременно философия бизнеса и активный процесс. Маркетинг — это социальный процесс, направленный на удовлетворение потребностей и желаний людей и организаций путем обеспечения свободного конкурентного обмена товарами и услугами, представляющими ценность для покупателя |
| Голубков Е. П. | Маркетинг — это процесс согласования возможностей компании и запросов потребителей. Маркетинг согласно его широкому пониманию — это социально-управленческий процесс, посредством которого индивидуумы и группа людей путем создания продуктов и их обмена получают то, в чем они нуждаются |
| Кафедра маркетинга СПбГУЭФ | Маркетинг — это философия и инструментарий взаимодействия хозяйствующих субъектов социально-экономической системы по поводу изучения, создания, воспроизводства и удовлетворения спроса конечных потребителей, их потребностей в товарах и услугах с целью получения прибыли или достижения иных результатов |
| Роджер Л. В. | Маркетинг отнюдь не начинается там, где завершается производство, — напротив, в его задачи входит определение характера и масштабов производства, а также путей рентабельного использования производственных мощностей фирмы и инженерно-технических возможностей с учетом перспектив сбыта. Другими словами, выработка решений в области маркетинга предшествует решениям в области производства и капиталовложений. Маркетинг можно определить как ведущую область хозяйственного управления, в функции которой входит организация и руководство всей совокупностью видов деятельности, связанных с превращением покупательской способности потребителей в эффективный спрос на специфическое изделие или услугу, а также с доведением этого изделия или услуги до конечного или промежуточного покупателя, чтобы обеспечить установленную компанией норму прибыли или достижение других целей |
| Мефферт X. | Современная обобщенная и одновременно широкая интерпретация маркетинга отождествляет маркетинг с любой формой обмена между двумя участниками сделки. Маркетинг — это ориентированное на рынок управление предприятием, которое заключается в планировании, координации и контроле всей деятельности предприятия, связанной с действующими и потенциальными рынками |
| Район У. | Маркетинг может быть еще определен как деятельность, включающая распознавание потребностей, создание товаров и услуг, удовлетворяющих эти потребности, равно как и формирование, а отсюда — расширение спроса на эти товары и услуги |
| Левит Т. | Маркетинг не следует отождествлять с продажей товаров. Если функция торговой системы состоит в том, чтобы убедить покупателя купить то, что уже произведено, задача маркетинга есть поставка на рынок того товара, в котором потребитель действительно нуждается. Коммерческие усилия по сбыту — это сосредоточенность на нуждах продавца, а маркетинг — это сосредоточенность на нуждах покупателя. Коммерческие усилия по сбыту — это забота о нуждах продавца по превращению его товара в наличные деньги, а маркетинг — это забота об удовлетворении нужд клиента посредством товара и целого ряда факторов, связанных с созданием, поставкой и, наконец, потреблением этого товара |
| Кулаков С. Н. | Суть современного маркетинга: это предпринимательская деятельность, превращающая потребности покупателя в доходы предприятия |
| Данилов-Даниэлян В. | Все то, что является объектом данной дисциплины, есть некая проекция предпринимательской деятельности на ось рынка |
| Характеристики организационной структуры | ||
| Маркетинговая оргкультура | Производственная оргкультура | |
| 1. У высшего руководства на первом месте... | ||
| ...потребности покупателя | ...потребности производителя | |
| 2. Иа самых высоких должностях находятся... | ||
| ...маркетологи, ибо они отвечают и за сбыт | ...инженеры, отвечающие, за производство | |
| 3. Производится и продается... | ||
| ...только то, что будет куплено | ...то, что возможно произвести | |
| 5. Формулирование целей предприятия... | ||
| ...на основе внешних факторов | ...на основе внутренних факторов | |
| 6. Горизонт перспективного планирования... | ||
| ...преимущественно долгосрочный | ...преимущественно краткосрочный | |
| 7. Главное внимание обращено... | ||
| ...на потребности покупателей | ...на издержки производства | |
| 8. Научные исследования направлены на... | ||
| ...анализ рынка, в том числе и конкурентов | ...усовершенствование техники | |
| 9. Ценовая политика строится на... | ||
| ...ценах рынка (с учетом конкуренции) | ...издержках производства | |
| 10. Разработка идей новых товаров идет на основе... | ||
| ...анализа потребностей рынка и других факторов внешней и внутренней среды | сокращения издержек производства прежних товаров без учета потребностей рынка | |
| 11. В конструировании новых товаров ведущая роль принадлежит... | ||
| ...дизайнерам | ...инженерам-конструкторам | |
| 12. Производственный процесс... | ||
| ...максимально гибок, ориентирован на быструю реакцию изменения потребностей покупателей и других факторов рынка | ...как правило, жесткий, ориентирован только на возможности производства | |
| 13. Упаковка рассматривается как средство... | ||
| ...в первую очередь рекламы и продвижения | ...сохранения товара и только | |
| 14. Конкурентоспособность рассматривается через... | ||
| ...призму «цены потребления» | ...в основном через призму цены продажи | |
| 15. Философия руководства выражается словами... | ||
| «Мы управляем не заводом, а маркетинговой организацией, удовлетворяющей потребности покупателей» | ...Г. Форда, говорившего о своем автомобиле модели «Т»: «Мы можем предложить Вам автомобиль любого цвета... При условии, что это цвет черный» |
Бюджетный процесс является составной частью бюджетного планирования, его главной формой. Бюджетное планирование как органическая часть финансового планирования подчинено требованиям финансовой политики государства. В ходе бюджетного планирования обеспечиваются централизованное распределение и перераспределение стоимости общественного продукта и национального дохода между звеньями финансовой системы, достигается воздействие финансов на основные экономические и качественные показатели государственных программ развития страны, выявление резервов эффективного использования материальных, трудовых и финансовых ресурсов.
Бюджетное планирование осуществляется уполномоченными законом органами государственной власти и включает бюджетный процесс, его нормативно-правовую базу и организационную основу, а также вопросы теории и методологии составления бюджетов государства. В качестве принципов бюджетного планирования выделяют, в частности, единство правового регулирования, непрерывность планирования годового бюджета, балансовый метод и др.
Бюджетный процесс как главная форма бюджетного планирования представляет собой регламентированную законодательством деятельность органов государственной власти, органов местного самоуправления и участников бюджетного процесса по составлению, рассмотрению, утверждению и контролю за исполнением федерального бюджета, бюджетов субъектов Федерации и местных бюджетов, а также бюджетов государственных внебюджетных фондов. Его содержание определяется государственным и бюджетным устройством страны, бюджетными правами соответствующих органов власти и юридических лиц.
Бюджетный процесс охватывает четыре стадии бюджетной деятельности:
* составление проектов бюджетов;
* рассмотрение и утверждение бюджетов;
* исполнение бюджетов;
* составление отчета об исполнении бюджетов и их утверждение.
Все стадии бюджетного процесса взаимообусловлены и взаимосвязаны и являются прямым отражением не только экономической жизни общества, но и политической культуры.
Составление, рассмотрение, утверждение и исполнение бюджетов разных уровней в России, а также контроль за их исполнением регулируются Конституцией Российской Федерации, Бюджетным кодексом Российской Федерации и другими законами РФ, законами республик в составе РФ, решениями государственных представительных органов власти субъектов Федерации, Правилами о порядке составления и исполнения бюджета, издаваемыми Министерством финансов РФ на основе бюджетного законодательства.
Участниками бюджетного процесса являются:
* Президент Российской Федерации;
* органы законодательной (представительной) власти;
* органы исполнительной власти (высшие должностные лица субъектов Федерации, главы местного самоуправления, финансовые органы, органы, осуществляющие сбор доходов бюджетов, другие полномочные органы);
* органы денежно-кредитного регулирования;
* органы государственного и муниципального финансового контроля;
* государственные внебюджетные фонды;
* главные распорядители и распорядители бюджетных средств;
* иные органы, на которые законодательством РФ, субъектов Федерации возложены бюджетные, налоговые и иные полномочия;
* бюджетные учреждения, государственные и муниципальные унитарные предприятия, другие получатели бюджетных средств, а также кредитные организации, осуществляющие операции со средствами бюджетов.
Основные задачи бюджетного процесса:
* выявление материальных и финансовых резервов государства;
* максимально приближенный к реальности расчет расходов бюджетов;
* обеспечение максимальной сбалансированности бюджетов;
* согласование бюджетов с реализуемой экономической программой;
* осуществление бюджетного регулирования в целях перераспределения источников доходов между бюджетами разного уровня, отраслями хозяйства, экономическими регионами и др.
Деятельность государства от начала составления государственного бюджета до утверждения отчета об его исполнении длится около трех лет, и этот срок называется бюджетным циклом. Весь бюджетный цикл делится на стадии бюджетного процесса.
Стадия составления, рассмотрения и утверждения бюджета охватывает период от начала составления (за 10 месяцев до начала финансового (бюджетного) года) до его утверждения (15 декабря текущего года). Стадия исполнения бюджета длится в течение финансового (бюджетного) года. Отчетная стадия об исполнении бюджета охватывает период составления правительством отчета и рассмотрения его в законодательном органе. Правительство представляет отчет в Государственную Думу и одновременно в Счетную палату не позднее 1 июня текущего года; Счетная палата проводит проверку отчета и готовит заключение по нему в течение 4,5 месяцев; Государственная Дума рассматривает отчет в срок 1,5 месяца после представления Счетной палатой заключения по нему.
Бюджет действует в течение одного года - с 1 января по 31 декабря. Финансовый (бюджетный) год на территории РФ длится 12 месяцев. По прошествии года по закону для завершения бюджета предоставляется еще один льготный месяц, в течение которого завершаются операции по обязательствам, принятым в рамках исполнения бюджета. Счетный период включает срок с 1 января по 31 декабря плюс льготный месяц.
Стадии бюджетного процесса следуют строго последовательно, и этот порядок изменению не подлежит. В то же время каждый раз работа с бюджетом начинается снова, так как ежегодно изменяется объем национального дохода государства, перераспределяются государственные средства в зависимости от задач, решаемых государством в данный период. Ежегодно изменяются потребности каждой республики в составе РФ, национально-государственных образований, административно-территориальных единиц, органов местного самоуправления в денежных средствах, что зависит от того, как будет развиваться хозяйство и социальная сфера данной территории в следующем году.
На каждой стадии бюджетного процесса решаются вопросы, которые не могут быть решены в другое время. Так, проблемы бюджетного регулирования за счет процентных отчислений от федеральных налогов и налогов республик в составе РФ решаются в момент составления бюджета.
Все стадии бюджетного процесса взаимосвязаны. Организует эту работу Правительство Российской Федерации. Оно начинает работу над проектом федерального бюджета не позднее, чем за 10 месяцев до начала очередного финансового года, определяет порядок и сроки составления проектов федерального бюджета, а также порядок работы над документами и материалами, обязательными для представления одновременно с проектом федерального бюджета.
На первом этапе формирования федерального бюджета осуществляется выбор Правительством РФ плана-прогноза социально-экономического развития Российской Федерации, разработка федеральными органами проекта федерального бюджета. Министерство экономического развития и торговли РФ организует и разрабатывает проект прогноза социально-экономического развития России на очередной финансовый год и уточняет параметры среднесрочного прогноза, который кладется в основу разработки перспективного финансового плана.
На основе выбранного Правительством РФ варианта плана-прогноза функционирования экономики Министерство финансов РФ организует и разрабатывает проектировки основных показателей федерального бюджета на среднесрочную перспективу и проект федерального закона о федеральном бюджете на очередной финансовый год.
После принятия Правительством РФ основных характеристик федерального бюджета на очередной финансовый год и распределения его расходов в соответствии с функциональной классификацией расходов бюджетов Министерство финансов РФ в двухнедельный срок: направляет бюджетные проектировки федеральным органам исполнительной власти для распределения по конкретным получателям средств федерального бюджета; уведомляет органы исполнительной власти субъектов Федерации о методике формирования межбюджетных отношений РФ и субъектов Федерации на очередной финансовый год и среднесрочную перспективу.
Второй этап формирования федерального бюджета включает распределение федеральными органами исполнительной власти предельных объемов бюджетного финансирования в соответствии с функциональной и экономической классификацией расходов по получателям бюджетных средств, а также разработку указанными органами предложений о проведении структурных и организационных преобразований в отраслях экономики и социальной сфере, приостановлении или отмене нормативных актов, исполнение которых влечет расходование средств, не обеспеченное реальными источниками финансирования в очередном финансовом году.
Одновременно Министерство экономического развития и торговли РФ формирует перечень федеральных программ, подлежащих финансированию, согласовывает их объемы на очередной финансовый год и среднесрочную перспективу. Несогласованные вопросы рассматриваются межведомственной правительственной комиссией, возглавляемой министром финансов.
Вся указанная работа второго этапа должна быть завершена не позднее 15 июля года, предшествующего финансовому году. С 15 июля по 15 августа Правительство РФ рассматривает: прогноз социально-экономического развития Российской Федерации на очередной финансовый год и уточнение параметров этого прогноза на среднесрочный период; проект федерального бюджета на очередной финансовый год, проект перспективного финансового плана и другие документы и материалы, характеризующие бюджетную финансовую политику, представленные Министерством экономического развития и торговли РФ, Министерством финансов РФ, другими федеральными органами исполнительной власти; утверждает проект федерального закона о федеральном бюджете.
Составленный и согласованный проект федерального бюджета РФ Правительство РФ не позднее 26 августа текущего года вносит на рассмотрение в Государственную Думу. Одновременно с проектом бюджета представляются следующие документы и материалы:
- предварительные итоги социально-экономического развития РФ за истекший период текущего года;
- прогноз социально-экономического развития РФ на очередной финансовый год;
- основные направления бюджетной и налоговой политики на очередной финансовый год;
- план развития государственного и муниципальных секторов экономики;
- прогноз сводного финансового баланса по территории РФ на очередной финансовый год;
- прогноз консолидированного бюджета РФ на очередной финансовый год;
- основные принципы и расчеты по взаимоотношениям федерального бюджета и консолидированных бюджетов субъектов Федерации в очередном финансовом году;
- проекты федеральных целевых программ и федеральных программ развития регионов, предусмотренных к финансированию из федерального бюджета на очередной финансовый год;
- проект федеральной адресной инвестиционной программы;
- проект программы приватизации государственных и муниципальных предприятий;
- расчеты по статьям классификации доходов федерального бюджета, разделам и подразделам функциональной классификации расходов бюджетов РФ и дефициту федерального бюджета на очередной финансовый год;
- проект программы государственных внешних заимствований РФ и предоставления государственных кредитов РФ иностранным государствам на очередной финансовый год;
- проект структуры государственного внешнего и внутреннего долга РФ, проект программы внутренних заимствований, предусмотренных на очередной финансовый год для покрытия дефицита федерального бюджета, и некоторые другие материалы.
Вместе с проектом федерального закона о федеральном бюджете Правительство РФ вносит в Государственную Думу проекты федеральных законов о внесении изменений и дополнений в законодательные акты о налогах и сборах, о бюджетах государственных внебюджетных фондов, законопроектов об увеличении минимального размера пенсий и минимального размера оплаты труда, о порядке индексации заработной платы работников бюджетной сферы и государственных пенсий, а также проектов законодательных актов об отмене правовых актов, исполнение которых влечет расходование бюджетных средств, не обеспеченные реальными источниками финансирования.
Кроме указанных выше документов и материалов, Правительство РФ представляет в Государственную Думу не позднее 1 октября текущего года: оценку ожидаемого исполнения федерального и консолидированного бюджета РФ за отчетный финансовый год; проекты программ предоставления гарантий Правительства РФ из средств федерального бюджета на очередной финансовый год на возвратной основе и отчеты о выполнении соответствующих программ за истекший период текущего финансового года; предложения по расходам на содержание Вооруженных Сил, других войск, воинских формирований и органов с указанием их штатной численности на начало и конец очередного финансового года; поквартальное распределение доходов и расходов федерального бюджета на очередной финансовый год.
Рассмотрение и утверждение бюджетов в законодательных органах - Федеральном Собрании (Парламенте) РФ, представительных органах субъектов Федерации и местного самоуправления.
Проект федерального бюджета и указанные выше документы, полученные Советом Государственной Думы, направляются в его Комитет по бюджету для заключения о соответствии представленных документов и материалов требованиям бюджетного законодательства. На основании заключения Комитета Совет Думы решает вопрос о принятии проекта федерального закона о федеральном бюджете к рассмотрению в Государственной Думе. Все материалы передаются Президенту РФ, Совету Федерации, комитетам Думы для внесения замечаний и предложений, а также в Счетную палату на заключение.
Комитеты, утвержденные Советом Государственной Думы, ответственны за рассмотрение отдельных разделов и подразделов расходов с точки зрения целесообразности, актуальности, финансовой и материальной возможностей. Результаты анализа и заключения по каждому комитету направляются в Комитет по бюджету.
Получив заключение от каждого комитета, Комитет по бюджету составляет сводное заключение по проекту федерального бюджета и представляет его на рассмотрение в Государственную Думу, которая начинает рассмотрение бюджета в четырех чтениях.
При рассмотрении федерального бюджета в первом чтении Государственная Дума обсуждает его концепцию и прогноз социально-экономического развития РФ, главные направления бюджета и налоговой политики, основные принципы и расчеты по взаимоотношениям федерального бюджета и бюджетов субъектов Федерации, проект программы государственных внешних заимствований в части источников внешнего финансирования дефицита федерального бюджета, а также основные характеристики федерального бюджета на предстоящий год, к которым относятся:
- доходы по группам, подгруппам и статьям классификации доходов бюджетов РФ;
- распределение доходов от федеральных налогов и сборов между федеральным бюджетом и бюджетами субъектов Федерации;
- дефицит федерального бюджета в абсолютных цифрах и в процентах к расходам, а также источники покрытия дефицита;
- общий объем расходов федерального бюджета в целом.
По результатам обсуждения принимается проект федерального бюджета в первом чтении и утверждаются основные характеристики федерального бюджета, после чего Государственная Дума не имеет права увеличивать доходы и дефицит бюджета, если на эти изменения отсутствует положительное заключение Правительства РФ.
В случае отклонения проекта федерального бюджета в первом чтении Государственная Дума может:
- передать указанный законопроект в Согласительную комиссию по уточнению основных характеристик федерального бюджета, состоящую из представителей Государственной Думы, Совета Федерации и Правительства, для разработки согласованного варианта;
1) вернуть законопроект в Правительство РФ на доработку;
2) поставить вопрос о доверии Правительству РФ.
При отклонении федерального бюджета и передаче его в Согласительную комиссию она разрабатывает вариант основных характеристик федерального бюджета и принимает согласованное решение. Согласованный текст федерального бюджета вновь вносится на рассмотрение в первом чтении в Государственную Думу.
Закон о бюджете считается одобренным Советом Федерации, если за него проголосовало более половины общего числа членов этой палаты либо если в течение 14 дней он не был рассмотрен Советом Федерации. В случае отклонения Советом Федерации этого закона обе палаты Парламента могут создать Согласительную комиссию для преодоления возникших разногласий, после чего федеральный закон подлежит повторному рассмотрению Думой в одном чтении.
В случае несогласия Государственной Думы с решением Совета Федерации закон о бюджете считается принятым, если при повторном голосовании за него проголосовало не менее 2/3 общего числа депутатов Думы (ст. 105 Конституции РФ).
Принятый федеральный закон о бюджете в течение 5 дней направляется Президенту РФ для подписания и обнародования. На подписание Закона Президентом отводится 14 дней. Если Президент в этот срок не подписал Закон и отклонил его, то Дума и Совет Федерации вновь рассматривают его в установленном Конституцией РФ порядке. Если при повторном рассмотрении закон о бюджете будет одобрен в ранее принятой редакции большинством - не менее 2/3 голосов общего числа членов Парламента, он подлежит подписанию Президентом РФ и обнародованию в течение 7 дней (ст. 107 Конституции РФ).
В случае непринятия федерального бюджета на очередной финансовый год до 1 декабря текущего года, а также в случае невступления в силу федерального закона о федеральном бюджете на очередной финансовый год по другим причинам до 1 января очередного года, Государственной Думой принимается федеральный закон о финансировании государственных расходов из федерального бюджета в первом квартале финансового года.
Вычислению многих пределов, содержащих неопределенности, часто помогает использование двух так называемых замечательных пределов:
1) 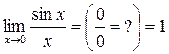 (x – угол в радианах)
(x – угол в радианах)
(1)
2) 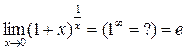 , где
, где  .
.
(в другом виде 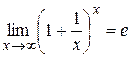 )
)
Докажем первый замечательный предел. Для этого вспомним школьную формулу для длины l произвольной дуги окружности (рис.1):
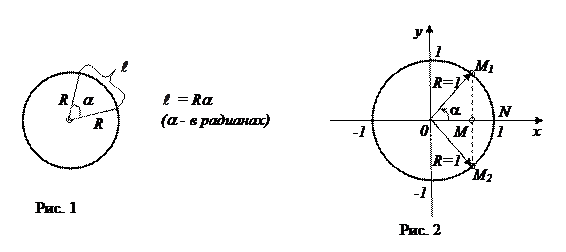
А теперь рассмотрим рис. 2:
 ;
;  ;
; 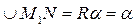 ;
;  ;
; 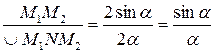 (
( – в радианах).
– в радианах).
При 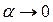 хорда M 1 M 2 и дуга M 1 NM 2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при
хорда M 1 M 2 и дуга M 1 NM 2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при 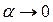 дробь
дробь  . А это и означает, что
. А это и означает, что
 (
( – угол в радианах)
– угол в радианах)
Полученный результат совпадает (при другом обозначении) с первым замечательным пределом (1).
Второй замечательный предел, приводит к важному для всей высшей математики числу e (к Неперову числу – по имени шотландского математика 16–го века Джона Непера, введшего в математику это число). Приведем доказательство.
Теорема 1: Переменная величина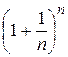 , где n - натуральное число, при
, где n - натуральное число, при  имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Доказательство: По формуле бинома Ньютона мы можем написать:

Произведем алгебраические преобразования.
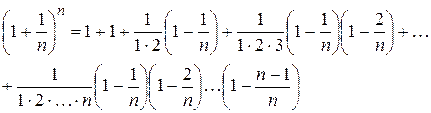 (2)
(2)
Из полученного равенства можно сделать вывод, что переменная величина 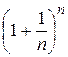 является возрастающей. Действительно,
является возрастающей. Действительно,
1) все члены разложения – положительны;
2) при переходе от значения n к (n+1) каждое слагаемое суммы возрастает, т.к. 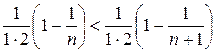 ;
;
3) добавляется ещё одно слагаемое.
Также переменная величина 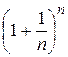 ограничена. Докажем этот факт. Учитывая, что
ограничена. Докажем этот факт. Учитывая, что  ;
;  и т.д., из (2) получаем
и т.д., из (2) получаем 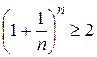 и
и
 .
.
Заметив, что  . Используем эти оценки и получим:
. Используем эти оценки и получим: 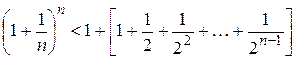 . Слагаемые в квадратных скобках образуют геометрическую прогрессию со знаменателем
. Слагаемые в квадратных скобках образуют геометрическую прогрессию со знаменателем  и первым членом
и первым членом  . Поэтому
. Поэтому 
 . Подытоживая все сказанное, получаем:
. Подытоживая все сказанное, получаем:  .
.
Итак, переменная величина 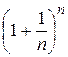 - возрастающая и ограниченная. На основании свойств пределов она имеет предел. Этот предел обозначим буквой е.
- возрастающая и ограниченная. На основании свойств пределов она имеет предел. Этот предел обозначим буквой е.
Теорема 2: Функция 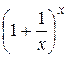 при
при  стремится к числу е.
стремится к числу е.
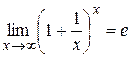 .
.
Доказательство: по теореме 1  , если n принимает целые положительные значения. Пусть теперь x стремится к бесконечности, принимая как дробные, так и отрицательные значения.
, если n принимает целые положительные значения. Пусть теперь x стремится к бесконечности, принимая как дробные, так и отрицательные значения.
1) Пусть 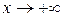 . Каждое его значение заключено между двумя положительными целыми числами
. Каждое его значение заключено между двумя положительными целыми числами  . При этом будут выполняться неравенства:
. При этом будут выполняться неравенства:

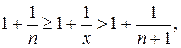
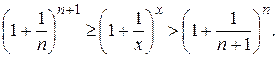
Если  , то
, то  . Найдем пределы переменных величин, между которыми заключена функция
. Найдем пределы переменных величин, между которыми заключена функция 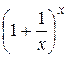 .
.
 .
.
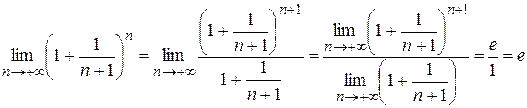 .
.
Следовательно, по свойствам пределов мы имеем 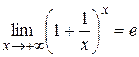 .
.
2) Пусть 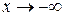 . Введем новую переменную t=-(x+1) или x=-(t+1). При
. Введем новую переменную t=-(x+1) или x=-(t+1). При 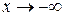 новая переменная
новая переменная  . Сделаем замену переменной и получим:
. Сделаем замену переменной и получим:

Что и требовалось доказать.
Число 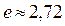 , как и число
, как и число  , принадлежит к числу важнейших математических констант. А такие функции, как
, принадлежит к числу важнейших математических констант. А такие функции, как  и
и  , принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция
, принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция  называется экспоненциальной, а ее график называется экспонентой. А логарифмическая функция
называется экспоненциальной, а ее график называется экспонентой. А логарифмическая функция  называется функцией натурального логарифма, а ее график называется натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию e назвали натуральным – от слова «natur» (природа).
называется функцией натурального логарифма, а ее график называется натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию e назвали натуральным – от слова «natur» (природа).

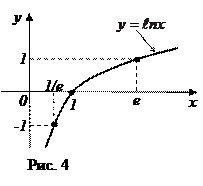
В математических справочниках имеются таблицы этих двух важных функций - и  , и
, и 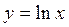 . Впрочем, для вычисления натуральных логарифмов
. Впрочем, для вычисления натуральных логарифмов 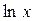 можно воспользоваться и таблицами общеизвестных десятичных логарифмов
можно воспользоваться и таблицами общеизвестных десятичных логарифмов  , если применить формулу перехода в логарифмах от одного основания к другому:
, если применить формулу перехода в логарифмах от одного основания к другому:
 ;
;
 (2.8)
(2.8)
При использовании замечательных пределов имеют в виду следующее обстоятельство: значение предела зависит от вида функции и того, к какому пределу стремится переменная, но не зависит от обозначения переменной.
Пример 1.  .
.
Пример 2.  ;
;
(при преобразованиях использовано обозначение  ).
).
Пример 3.  ;
;
(при преобразованиях использовано обозначение  ).
).
Пример 4.  .
.
Пример 5.  .
.
Пример 6. Найти 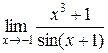 .
.
Используя формулу суммы кубов, преобразуем выражение под знаком предела: 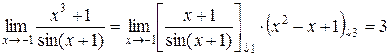 .
.
Пример 7. Найти  .
.
Решение.

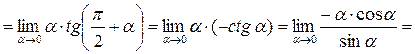
 .
.
Пример 8. Найти  .
.
Решение. 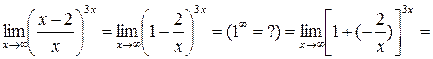
=| введем обозначение:  (
( ); тогда
); тогда  ;
;  |=
|=
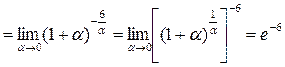 .
.
Пример 9: Найти  .
.
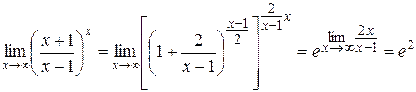
Пример 10: Найти 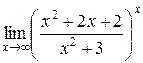 .
.

Пример 11: Найти 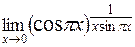 .
.
Чтобы подогнать структуру этого предела под структуру второго замечательного предела в основании степени прибавим и вычтем 1.

Выведем формулу, удобную для нахождения пределов в случае применения второго замечательного предела (неопределенности вида 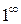 ). Пусть
). Пусть  . Здесь a может быть любым конечным числом или
. Здесь a может быть любым конечным числом или 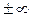 . Рассмотрим предел степени этих функций:
. Рассмотрим предел степени этих функций:

Итак, 
Пример 12. Найти 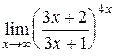 .
.
Проверим: 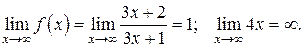
Найдем 
Тогда 
Пример 13. 
Пример 14. 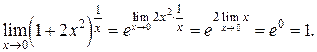
Пример 15. 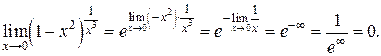
Для самостоятельного решения:
1. Найти  . Ответ:
. Ответ: 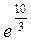 .
.
2. Найти  . Ответ:
. Ответ:  .
.
3. Найти 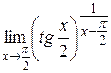 . Ответ: е.
. Ответ: е.
4. Найти  . Ответ:
. Ответ: 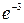 .
.
5. Найти  . Ответ: -4/5.
. Ответ: -4/5.
6. Найти  . Ответ:
. Ответ:  .
.
7. Найти 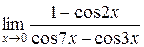 . Ответ: -1/10.
. Ответ: -1/10.
Кроме уже упомянутых первого и второго замечательных пределов, существует целый список пределов аналогичных ему по структуре и использованию:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 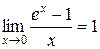 ;
;
8)  ;
;
9)  ;
;
10)  .
.
11)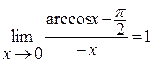 .
.
К этому списку полезно помнить следующие тригонометрические тождества: 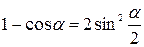 ;
;  .
.
Принцип использования этого списка очень прост: нужно подогнать структуру в искомом пределе под структуру соответствующего выражения в табличном пределе. Все необходимые сомножители либо выделяются из имеющегося выражения, либо приобретаются путем умножения и деления на него, либо выделяются с помощью преобразований исходного выражения. Приведем доказательство некоторых пределов из этого списка.
а) 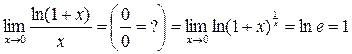 – согласно (2.7);
– согласно (2.7);
б)  ;
;
в) 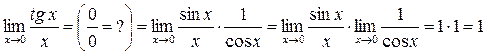 ;
;
г) 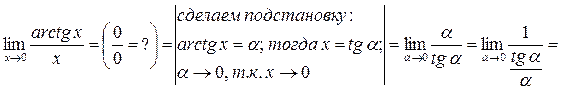
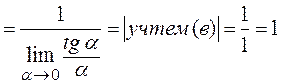 ;
;
д) 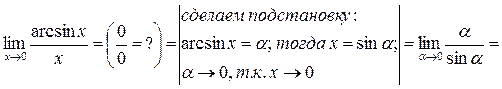
 ;
;
е) 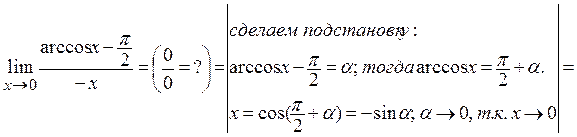
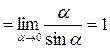 .
.
Часто перед тем, как применить табличные пределы, нужно провести какие-либо дополнительные, уже описанные ранее, стандартные преобразования или сделать замену переменной. Рассмотрим пример, в котором нужно избавиться от иррациональности.
Пример 16 Найти  .
.
Для того, чтобы избавиться от иррациональности в знаменателе, нужно умножить числитель и знаменатель на 

Другое стандартное преобразование «плюс-минус единица» встречается на практике в примерах, содержащих логарифмы и степенные функции. В этих случаях логарифмируемое выражение и основание степенной функции при 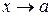 действительно стремится к 1, но они задаются в таком виде, где постоянное слагаемое 1 отсутствует. Чтобы пользоваться табличными пределами, нужно преобразовать логарифмируемое выражение и основание степени к требуемому виду. Для этого и используется стандартное преобразование «плюс-минус единица». При этом мы явно получаем 1 и выражение
действительно стремится к 1, но они задаются в таком виде, где постоянное слагаемое 1 отсутствует. Чтобы пользоваться табличными пределами, нужно преобразовать логарифмируемое выражение и основание степени к требуемому виду. Для этого и используется стандартное преобразование «плюс-минус единица». При этом мы явно получаем 1 и выражение  , что позволит далее использовать табличные пределы.
, что позволит далее использовать табличные пределы.
Пример 17: Найти  .
.

Пример 18:Найти  .
.
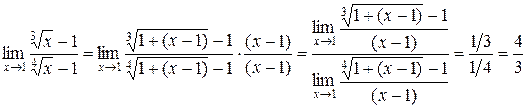 .
.
Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную, и из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной. Рассмотрим пример, в котором наиболее целесообразным представляется замена переменной.
Пример 19: Найти  .
.
При  не существует предела
не существует предела 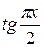 . Сделаем подстановку:
. Сделаем подстановку:  . Когда
. Когда  , то новая переменная
, то новая переменная 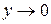 , так как
, так как 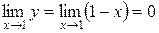 . Если
. Если  , то
, то  ; выражение, стоящее под знаком предела перепишется так:
; выражение, стоящее под знаком предела перепишется так: 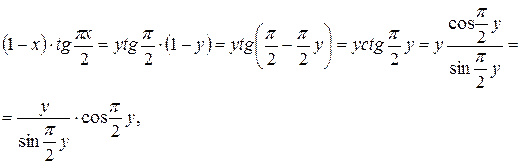
поэтому 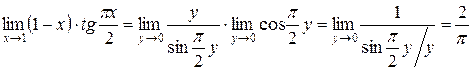
Табличные пределы можно использовать для вычисления других пределов при раскрытии неопределенностей вида 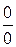 , заменяя одни функции на им эквивалентные бесконечно малые. Функции
, заменяя одни функции на им эквивалентные бесконечно малые. Функции  называются эквивалентными бесконечно малыми при
называются эквивалентными бесконечно малыми при 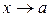 , если
, если 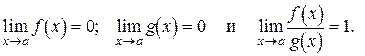 Другими словами эквивалентность означает выполнение предельного равенства. Эквивалентность двух функций обозначается волнистой чертой:
Другими словами эквивалентность означает выполнение предельного равенства. Эквивалентность двух функций обозначается волнистой чертой:  .
.
При раскрытии неопределенности функцию или функции, входящие в предел, можно заменить на им эквивалентные:


Замена во втором случае возможна, если 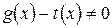 . Используя замечательные пределы, можно составить таблицу эквивалентных бесконечно малых.
. Используя замечательные пределы, можно составить таблицу эквивалентных бесконечно малых.
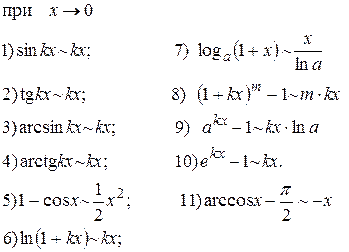 (3)
(3)
Приведем несколько примеров использования эквивалентных функций при вычислении пределов.
Пример 20.
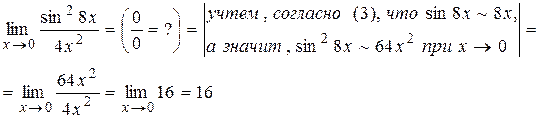
Пример 21.

Пример 22.
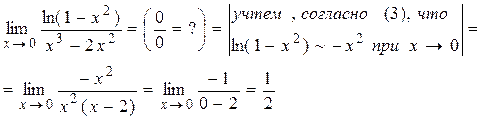
Пример 23. 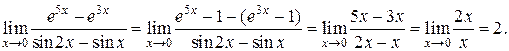
Пример 24.
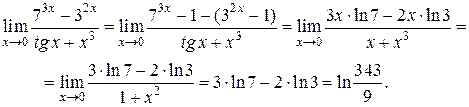
Пример 25.
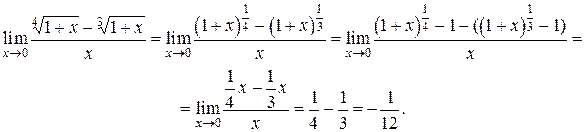
Пример 26. 
Для самостоятельного решения:
1. Найти  . (1/2).
. (1/2).
2. Найти  . (
. ( ).
).
3. Найти  . (
. (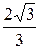 ).
).
4. Найти  . (1/е).
. (1/е).
5. Найти  . (1/2).
. (1/2).
6. Найти  . (1).
. (1).
7. Найти  . (1).
. (1).
8. Найти 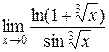 . (1).
. (1).


Рис. ____ Укрупненная структурная схема системы управления
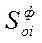
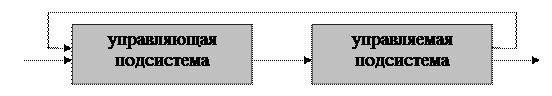
Рис. _____ Реализация обратной связи.

Рис. ____ Структурная схема системы автоматического управления
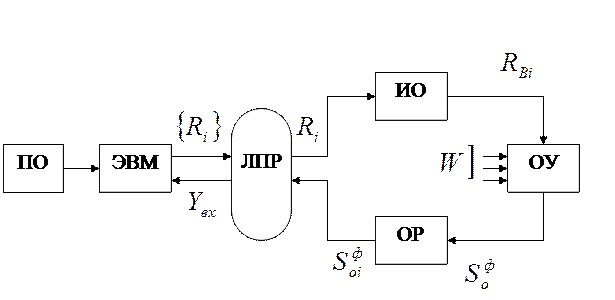
Рис. ___ Структурная схема автоматизированных информационных систем (АИС).
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 373; Нарушение авторских прав?; Мы поможем в написании вашей работы!