Экспериментальные изотермы. Критические состояния

Уравнение Ван-дер-Ваальса – алгебраическое уравнение третьей степени относительно объема. Для одного моля газа

.

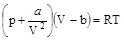Раскрыв скобки и расположив члены уравнения по убывающим степеням объема, можно записать последнее в следующем виде:

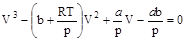. (9.1)

Это уравнение третьей степени относительно объема и, следовательно, при данных р и Т оно может иметь или три вещественных корня, или один вещественный и два комплексно-сопряженных корня, не имеющих физического смысла. Это зависит от соотношения между коэффициентами. При низких температурах уравнение имеет три вещественных корня и график p=f(V) имеет вид, изображенный на рис.9.4.

р     рнп   жид- кость жидкость + газ газ   V1 V2 V3 V   Рис.9.4

Для того, чтобы полу-чить изотерму опытным путем, нужно взять вещест-во в газообразном состоя-нии, поместить его в сосуд с перемещающимся порш-нем и начать медленно сжимать, делая одновре-менно отсчеты давления и объема, а также, следя за тем, чтобы температура вещества оставалась посто-янной. Результат подоб-ного опыта дан на рис.9.4 (жирная линия).

Вначале с уменьшением объема давление газа растет, причем ход изотермы хорошо описывается уравнением Ван-дер-Ваальса (9.1).

Однако, начиная с некоторого объема V₃, экспериментальная изотерма перестает следовать уравнению (9.1). Начиная с этого значения объема, давление в сосуде перестает изменяться, само вещество перестает быть однородным, часть газа конденсируется в жидкость. Происходит расслоение вещества на две фазы: жидкую и газообразную.

По мере дальнейшего уменьшения объема все большая часть вещества переходит в жидкую фазу, причем переход осуществляется при постоянном давлении, обозначенном на рисунке р_нп. После того, как процесс конденсации вещества в жидкость заканчивается при V=V₁, дальнейшее уменьшение объема сопровождается быстрым ростом давления. При этом ход изотермы снова примерно следует уравнению (9.1). Вещество в состояниях, соответствующих этому участку изотермы, снова будет однородным, но представляет собой не газ, а жидкость.

Таким образом, уравнение Ван-дер-Ваальса описывает не только газообразное состояние вещества, но охватывает также процесс перехода в жидкое состояние и процесс сжатия жидкости.

Сопоставление экспериментальной изотермы с изотермой Ван-дер-Ваальса дает, что эти изотермы довольно хорошо совпадают на участках, отвечающих однофазным состояниям вещества, но ведут себя совершенно различным образом в области расслоения на две фазы. Вместо S-образного завитка на изотерме Ван-дер-Ваальса экспериментальная изотерма имеет в этой области прямолинейный горизонтальный участок.

В состояниях, соответствующих горизонтальному участку изотермы, наблюдается равновесие между жидкой и газообразной фазами вещества. Газ, находящийся в равновесии со своей жидкостью, называется насыщенным паром. Давление р_нп, при котором может существовать равновесие при данной температуре, называется давлением насыщенного пара.

Опыт показывает, что с повышением температуры (T¢<T¢¢<T¢¢¢<T_к) горизонтальный участок изотермы сокращается и при некоторой температуре он стягивается в точку. Называется эта температура критической (рис.9.5). При этом уменьшается различие в удельных объемах, а следовательно, и в плотностях жидкости и насыщенного пара.

р_нп

К

р¢¢¢_нп

Т_к

р¢¢_нп Т¢¢¢

Т¢¢

р¢_нп Т¢

Рис.9.5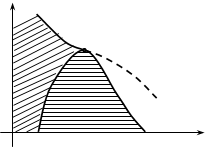

р   К Ж   Ж+П П     V Рис.9.6

При критической температуре это различие исчезает. Одновременно исчезает всякое различие между жидкостью и паром. Если провести линию через крайние точки горизонтальных участков изотерм, получается колокообразная кривая, ограничивающая область двухфазных состояний вещества. Колокообразная кривая и участок критической изотермы, лежащий слева от точки К делит диаграммы(pV) на три области (рис.9.6).

Наклонной штриховкой помечена область однородных жидких состояний. Под колокообразной кривой располагается область двухфазных состояний и область, лежащая справа от колокообразной кривой и верхней ветви критической изотермы, представляет собой область однородных газообразных состояний вещества. Особо следует отметить область, лежащую под правой ветвью критической изотермы – область пара.

Состояние вещества в этой области отличается от остальных газообразных состояний в том отношении, что при изотермическом сжатии вещество, находящееся в этом состоянии, претерпевает процесс сжижения. Вещество, находящееся в газообразном состоянии при температуре выше критической, не может быть сжижено никаким сжатием.

р_кр К

p¢¢_нс Т¢¢¢

Т_к

p¢_нп

Т¢¢

Т¢

V₁ V₂ V₃

Рис.9.7

Рассмотрим изотермы Ван-дер-Ваальса для нескольких значений температуры (рис.9.7). Расчеты показывают, что при температуре T¢ коэффициенты в уравнении (9.1) таковы, что все три решения уравнения оказыва-ются вещественными. С повы-шением температуры различие между тремя вещественными решениями уравнения (9.1) уменьшаются. Начиная с опре-деленной, своей для каждого ве- щества, температуры Т_кр, при

любом давлении вещественным остается только одно решение, соответствующее точке К. Температура называется критической температурой. Точка К называется критической точкой. Для соответствующей изотермы точка К служит точкой перегиба. Ей соответствуют три совпадающих вещественных решения уравнения (9.1). Касательная к критической изотерме в точке К является пределом, к которому стремятся секущие p¢ и p¢¢ при приближении температуры к критической. Следовательно, эта касательная, как и все секущие параллельна оси V так, что производная 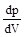в точке К равна нулю.

Кроме того, в точке перегиба должна быть равна нулю и вторая производная 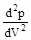. Разрешим уравнение (9.1) относительно

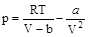. (9.2)

Дифференцирование этого выражения по V дает

;

.

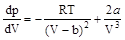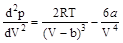В критической точке при Т=Т_кр и V=V_кр эти выражения обращаются в ноль:

;

.

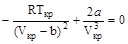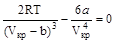Соответствующие значения и р_кр носят название критического объема и критического давления для данного вещества. Из уравнения (9.2) находим

.

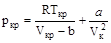Решая систему трех уравнений с тремя неизвестными V_кр, p_кр и Т_кр, получим

V_кр = 3b;

p_кр =;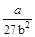

Т_кр =.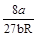

Таким образом, зная константы Ван-дер-Ваальса a и b, можно найти соответствующие критической точке V_кр, p_кр и Т_кр, которые называют критическими величинами. И наоборот, по известным критическим величинам могут быть найдены значения констант Ван-дер-Ваальса.

Дата добавления: 2013-12-14