Изучение динамики средней заработной платы и фонда заработной платы

Из определения средней заработной платы следует следующее ра­венство:

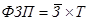
где ФЗП— фонд заработной платы в целом по статистической совокупности (совокупности работников, бригад, предприятий и т. д.)

и Т - средняя заработная плата и средняя списочная численность работ­ников (или отработанное время) изучаемой статистической совокупности.

Индексы названных трёх показателей связаны аналогично:

Это означает:

и, следовательно, абсолютное изменение фонда заработной платы со­ставит:

• за счёт изменения двух факторов - среднего уровня заработной платы и среднесписочной численности работников:

• за счёт изменения только средней заработной платы:

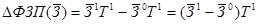
• за счёт изменения только средней списочной численности ра­ботников:

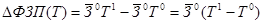
При этом будет соблюдаться равенство

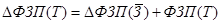
Пример. По предприятию имеются данные за два периода:

Показатели	Базисный период	Текущий период
Средняя заработная плата, руб.
Средняя списочная численность работников, человек

1. Фонд заработной платы за каждый период рассчитаем по формуле:

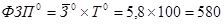тыс. рублей

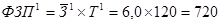тыс. рублей

2. Индексы всех трёх показателей

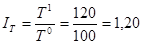
Следовательно, увеличение средней заработной платы на 3,4% и рост численности работников предприятия на 20% привело к росту фон­да заработной платы на 24,1%.

3. Абсолютный прирост фонда заработной платы составил:

тыс. руб.

В том числе за счёт изменения среднего уровня заработной платы

тыс. рублей

за счёт изменения только средней списочной численности работников:

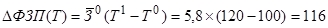тыс. руб.

Для оценки динамики уровня средней заработной платы применя­ется система трёх индексов: индексов переменного и постоянного со­става, индекса структуры.

Индекс заработной платы переменного состава представляет со­бой отношение средних уровней заработной платы в сравниваемых периодах:

Если в эту формулу подставить вместо выражение из формулы, то индекс переменного состава примет вид:

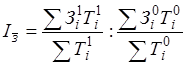или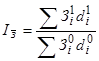

Индекс переменного состава заработной платы характеризует из­менение среднего уровня заработной платы за анализируемый период в зависимости от изменения заработной платы отдельных категорий ра­ботников (на отдельных предприятиях или в различных отраслях) и удельного веса численности работников с различным уровнем оплаты труда.

Абсолютное изменение среднего уровня заработной платы опреде­ляется по одной из следующих формул:

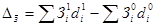
Индекс постоянного состава заработной платы оценивает динами­ку её среднего уровня под воздействием только одного фактора: изменения уровня заработной платы работников отдельных категорий. При этом предполагается, что структура работников (по уровню оплаты) была одинаковой в обоих сравниваемых периодах.

Формула расчёта индекса постоянного состава заработной платы выглядит следующим образом:

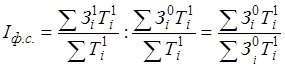или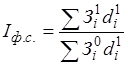

Разность между числителем и знаменателем показывает экономию (перерасход) фонда заработной платы в результате изме­нения среднего уровня заработной платы отдельных категорий ра­ботников.

Разность между числителем и знаменателем показывает, как изменился бы средний уровень заработной платы по предприятию в целом, если бы структура работников (по уровню заработной платы) была постоянной, и изменения наблюдались только в уровне заработной пла­ты отдельных категорий работников:

Если необходимо оценить влияние структурного фактора (измене­ния доли работников с разным уровнем заработной платы) на динамику среднего уровня заработной платы по предприятию в целом, то рассчи­тывается индекс структурных сдвигов:

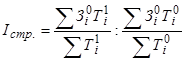или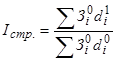

Разница между делимым и делителем формулы, а так же разница между числителем и знаменателем формулы представ­ляют абсолютное изменение средней заработной платы за счёт измене­ния только структуры работников по уровню заработной платы.

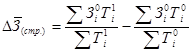
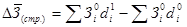
Индексы переменного, постоянного состава и структуры заработ­ной платы связаны следующим образом:

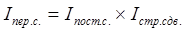
Для соответствующих абсолютных приростов выполняется следу­ющее равенство:

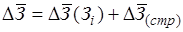
При однонаправленном действии каждого из рассматриваемых факторов может быть рассчитана доля прироста средней заработной платы за счёт:

• изменения заработной платы

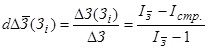
• изменения структуры работников

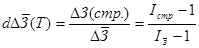
Пример. В таблице представлены данные о заработной плате и числен­ности работников трикотажной фабрики за 2 года.

Категории работников	Среднесписочная численность работников, человек	Среднемесячная заработная плата, тыс. рублей
Рабочие			4,5	5,0
Инженерно-технические работники			4,8	5,0
Аппарат управления			5,5	5,7

1. Индекс заработной платы переменного состава рассчитаем по фор­муле:

Следовательно, средняя зарплата на фабрике за год выросла на 9,6% или в соответствии с формулой на 0,45 тыс. рублей.

2. Индекс заработной платы постоянного состава рассчитаем по фор­муле:

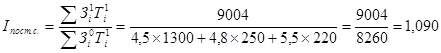
Этот индекс означает, что за счёт изменения заработной платы отдель­ных категорий работников, средняя заработная плата выросла на 9%.

Абсолютное изменение средней заработной платы за счёт измене­ния её уровня по отдельным категориям работников составило 0,42 тыс. рублей.

3. Индекс структуры определим по формуле:

Абсолютный прирост средней заработной платы за счет изменения струк­туры работников составил 0,03 тыс. рублей (4,67-4,64).

Проверим выполнение равенств:

Дата добавления: 2013-12-14