
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Середні величини
|
|
|
|
Найбільш поширеною формою статистичних показників, що використовуються в соціально-економічних дослідженнях, є середня величина. Вона представляє собою узагальнюючу кількісну характеристику ознаки в статистичній сукупності. Показник в формі середньої величини відображає типові риси і надає узагальнюючу характеристику однотипних явищ за однією варіативною ознакою. Він відбиває рівень цієї ознаки, віднесений до одиниці сукупності.
У статистичній практиці середні величини поділяють на два великі класи:
· ступеневі середні;
· структурні середні.
До ступеневих середніх відносять такі найбільш відомі види як середня геометрична, середня арифметична та середня квадратична. Як структурні середні розглядаються мода і медіана.
Ступеневі середні в залежності від форми надання вихідних даних можуть бути простими або зваженими.
Проста середня величина розраховується за не згрупованими даними і має наступний загальний вигляд:
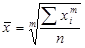 ,
,
де xi – індивідуальне значення варіативної ознаки (варіанта);
m – показник ступеня середньої;
n – число варіант.
Зважена середня розраховується за згрупованими даними і має загальний вигляд:
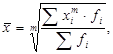
де xi – варіанта (значення) варіативної ознаки або серединне значення інтервалу, в якому вимірюється варіанта;
m – показник ступеня середньої;
fi – частота, яка показує скільки разів зустрічається і -те значення ознаки.
В залежності від того, яке значення приймає показник ступеня (m), розрізняють наступні види ступеневих середніх (табл. 4.3.).
Таблиця 4.3.
Види ступеневих середніх
| Вид ступеневої середньої | Показник ступеня | Формула розрахунку | |
| Проста | Зважена | ||
| Середня гармонійна | m= - 1 | 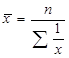
| 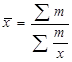 , m=xf , m=xf
|
| Середня геометрична | m→0 | 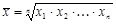
| 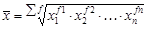
|
| Середня арифметична | m=1 | 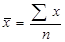
| 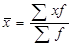
|
| Середня квадратична | m=2 | 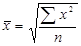
| 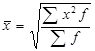
|
| Середня кубічна | m=3 | 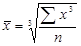
| 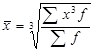
|
При вивченні закономірностей розподілу застосовують середню арифметичну, варіації – середню квадратичну, інтенсивності розвитку – середню геометричну. Різні види середніх, обчислені для одних і тих же даних, мають різну величину. Співвідношення між ними має наступний вигляд і називається правилом мажорантності середніх (тобто при збільшенні показника ступеня т збільшується і відповідна середня величина):
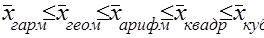 .
.
В статистичній практиці частіше, ніж інші види середніх, використовують середню арифметичну та середню гармонійну.
Середня арифметична – одна з найбільш поширених, застосовується в тих випадках, коли обсяг варіативної ознаки для всієї сукупності є сумою індивідуальних значень її окремих елементів.
Приклад. Статутний фонд акціонерної компанії сформований 6 засновниками; розмір внеску кожного з них становить, грн.. грн.: 6; 10; 12; 9; 7; 4. Середній внесок одного засновника:
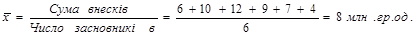
Так, за результатами складання іспиту студентами групи (табл. 4.4.)
Таблиця 4.4.
| Оцінка знань студентів, балів | xj | Разом | ||||
| Кількість оцінок | fj | |||||
| Питома вага оцінок, % | dj | 26,7 | 40,0 | 20,0 | 13,3 |
На основі частот: 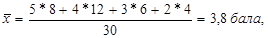
на основі часток: 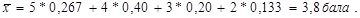
Середня хронологічна розраховується при аналізі показників, які задані дискретно, тобто у формі величин, що характеризують явище на пені моменти часу, певні дати.
Якщо показники характеризують аналізоване явище за період, розбитий на рівні проміжки часу, то середня величина у таких випадках визначається як середня хронологічна 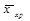 за формулою:
за формулою:
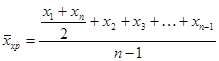 ,
,
де п – число моментів.
Приклад. У комерційному банку сума кредиторської заборгованості на початок кожного кварталу становила, млн. гр. од.: 1.01. – 20; 1.04. – 26; 1.07. – 32; 1.10. – 29; 31.12. – 22. Середньоквартальна сума кредиторської заборгованості складає:
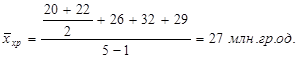
Середня гармонійна застосовується в тих випадках, коли нам не відомі самі варіанти, а відомі або їхні обернені числа (тоді використовується середня гармонійна проста), або добуток одиниць сукупності на значення ознаки (тобто m=x*f) (тоді використовують середню гармонійну зважену).
Середню гармонійну використовують, наприклад, для визначення середніх затрат праці, часу, матеріалів на одиницю продукції, на одну деталь за двома (трьома тощо) підприємствами, робітниками, які зайняти виготовленням одного й того ж виду продукції, однієї й тієї ж деталі.
Приклад. Маємо дані про витрати часу в годинах на виготовлення однієї деталі кожним з трьох робітників: ½, 1/3, 1/7. Треба обчислити середні витрати часу на виготовлення однієї деталі.
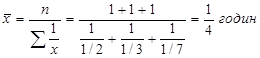
Приклад. Три промислових підприємства виробляють міксери. Собівартість виробництва міксера на 1-му підприємстві – 50 грн., на 2-му – 30 грн., на 3-му – 60 грн. визначити середню собівартість виробництва міксера за умови, що витрати на виробництво на 1-му підприємстві складають 600 грн., на 2-му – 660 грн., на 3-му – 900 грн.
Якби кожне з підприємств випускало б по одному міксеру, то можна було б застосувати формулу середньої арифметичної 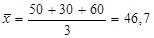 грн., але це не так, а тому:
грн., але це не так, а тому:
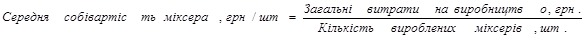
Використовуючи формулу середньої гармонійної зваженої, розрахуємо середню собівартість 1-го міксера:
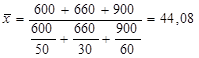 грн.
грн.
Середня геометрична найчастіше використовується для розрахунку середнього значення за індивідуальними відносними показниками динаміки.
Середня геометрична визначається як добуток відносних величин динаміки хі, які є кратним співвідношенням і -го значення показника до попереднього (і -1). Формула середньої геометричної:
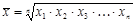 ,
,
де п – число осереднюваних величин.
Приклад. Кількість зареєстрованих злочинів за чотири роки зросла у 1,57 рази, у тому числі за перший рік – у 1,08; за другий – у 1,1; за третій – у 1,18; за четвертий – у 1,12 рази. Середньорічний темп зростання кількості зареєстрованих злочинів становить:
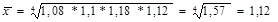 рази, тобто число зареєстрованих злочинів зростало щорічно у середньому на 12 %.
рази, тобто число зареєстрованих злочинів зростало щорічно у середньому на 12 %.
Для осереднення ознак рангової шкали застосовують нормований середній бал. Спочатку слід ранжирувати значення ознаки в порядку зростання якості.
Нормований середній бал обчислюється за формулою:
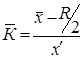 ,
,
де 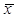 - середньозважений ранг відповідей (
- середньозважений ранг відповідей (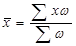 , де х – ранг,
, де х – ранг, 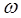 - частка відповідей, %);
- частка відповідей, %);
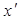 - середина шкали рангів (
- середина шкали рангів (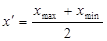 );
);
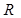 - розмах шкали рангів (
- розмах шкали рангів (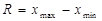 )
)
Приклад. Визначити середній бал якості відеокліпів, що демонструвалися по телебаченню, використовуючи такі дані:
| Рівень якості відеокліпів | Кількість відповідей, % до підсумку, 
| Ранг, х |
| Дуже висока Висока Середня Нижча за середню Низька | ||
| Разом | -- |
Рішення:
Нормований середній бал обчислюється за формулою:
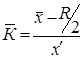 ,
,
де 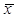 - середньозважений ранг відповідей:
- середньозважений ранг відповідей:
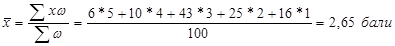 ;
;
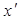 - середина шкали рангів:
- середина шкали рангів:
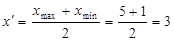 ;
;
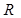 - розмах шкали рангів:
- розмах шкали рангів:
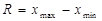 = 5-1= 4.
= 5-1= 4.
Тож, нормований середній бал дорівнює:
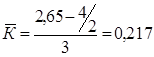 , або 21,7%
, або 21,7%
Структурні середні. Особливий вид середніх величин – структурні середні – використовують для вивчення внутрішньої побудови рядів розподілу. Найчастіше використовують показники моди й медіани.
Мода (Мо) – це значення варіанти, яка найчастіше повторюється в ряді розподілу. У дискретному ряді моду легко відшукати візуально за максимальною частотою, або часткою. Наприклад, в результаті опитування населення щодо самовизначення матеріального стану за чотирма градаціями (добрий, задовільний, незадовільний, нестерпний) більшість респондентів визначили свій стан як незадовільний. Або у розподілі сучасних сімей за кількістю дітей найпоширенішими є малодітні сім’ї, що мають одну дитину. Зустрічаються ряди, що мають дві моди (бімодальний ряд) або декілька (полімодальний). Наприклад, на фондовому ринку однаково високим попитом користуються як найдешевші акції, так і дорогі. В інтервальному ряді легко відшукати модальний інтервал, а приблизне значення моди обчисляють за формулою:

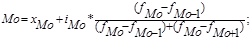
де хМо – нижня межа модального інтервалу;
іМо – велична (розмір) модального інтервалу;
fMo – частота модального інтервалу;
fMо-1 – частота передмодального інтервалу;
fMo+1 – частота післямодального інтервалу.
Медіана (Ме) – варіанта, яка припадає на середину упорядкованого ряду розподілу і ділить його на дві рівні за обсягом частини. Так, якщо в ряді розподілу робітників за віком Ме =34, то це означає, що половина з них менші за цей вік, половина – старші цього віку. У дискретному ряді для знаходження медіани обчислюють півсуму частот, і визначають значення ознаки, для якої накопичена частота (частка) дорівнює або перевищує половину обсягу сукупності. В інтервальному ряду в такий спосіб визначається медіанний інтервал, а значення медіани в інтервалі визначається за формулою:
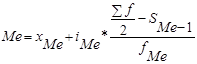 ;
;
де xMe – нижня межа медіанного інтервалу;
iMe – величина (розмір) медіанного інтервалу;
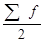 - півсума частот;
- півсума частот;
SMe-1 – сума накопичених частот перед медіанного інтервалу;
fMe – частота медіанного інтервалу.
За даними таблиці 4.5.найбільшими попитом користуються акції з терміном обертання в інтервалі 4 – 6 місяців. Це модальний інтервал, ширина якого іМо =2, а нижня межа хМо =4, частота fMo =29, передмодальна частота fMo-1 =13, а післямодальна частота fMo+1 =22. Модальний термін обертання облігацій становить:

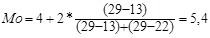 міс.
міс.
Таблиця 4.5.
| Термін обертання, місяців, х | Кількість проданих держоблігацій, тис., fi | Накопичена сума частот, тис., 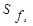
| хі | хіfi |
| До 2 2 – 4 4 – 6 6 – 8 8 – 10 10 і більше | ||||
| Разом | Х | Х |
Сума накопичених частот 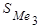 =57 визначає, що п’ятидесята з початку ряду облігація знаходитиметься в інтервалі 4 – 6 з частотою fMe =29. медіанний термін обертання проданих облігацій становить:
=57 визначає, що п’ятидесята з початку ряду облігація знаходитиметься в інтервалі 4 – 6 з частотою fMe =29. медіанний термін обертання проданих облігацій становить:
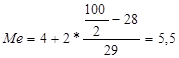 міс.
міс.
Тож половина облігацій продавалися з терміном обертання менше, ніж півроку – 5,5 міс., а половина – більше 5,5 міс.
У симетричних рядах розподілу значення моди та медіани збігаються з середньою величиною (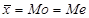 ).
).
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 991; Нарушение авторских прав?; Мы поможем в написании вашей работы!