Показники варіації

Варіація ознаки є властивістю статистичної сукупності і зумовлена дією безлічі взаємопов’язаних причин, серед яких є основні і другорядні. Основні формують центр розподілу, другорядні – варіацію ознаки, сукупна їх дія – форму розподілу.

Конкретні умови, в яких знаходиться кожний з об’єктів, що вивчається, а також особливості їхнього власного розвитку (соціальні, економічні тощо) виражаються відповідними числовими рівнями статистичних показників. Таким чином, варіація, тобто незбіг (несовпадение) рівнів одного й того ж показника у різних об’єктів, має об’єктивний характер і допомагає пізнати сутність явища, що вивчається.

Дослідження варіації в статистиці та соціально-економічних дослідженнях має велике значення, тому що величина варіації ознаки в статистичній сукупності характеризує її однорідність.

В статистичній практиці для вивчення та вимірювання варіації використовують різноманітні показники варіації в залежності від поставленого завдання. До них відносяться розмах варіації, середнє лінійне відхилення, середній квадрат відхилень (дисперсія), середнє квадратичне відхилення і коефіцієнт варіації.

Розмах варіації (R) є найпростішим вимірювачем варіації ознаки. Це різниця між найбільшим і найменшим значенням ознаки:

.

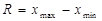Однак розмах варіації показує лише крайні значення ознаки. Повторюваність проміжних значень не враховується.

Середнє лінійне відхилення ( 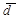) представляє собою середню величину із відхилень варіантів ознаки від їхньої середньої. Його можна розрахувати за формулою середньої арифметичної простої або зваженої в залежності від відсутності або наявності часток в ряду розподілу.

- просте середнє лінійне відхилення,

- зважене середнє лінійне відхилення,

де x_s – і -тий варіант ознаки;

f_s – питома вага і -того варіанту;

n – кількість варіантів;

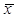- середня арифметична величина.

Показник середнього лінійного відхилення знайшов широке застосування на практиці. За його допомогою аналізуються, наприклад, склад працюючих, ритмічність виробництва, рівномірність постачань матеріалів, розробляються системи матеріального стимулювання.

Треба пам’ятати, що алгебраїчна сума відхилень від середнього рівня дорівнює нулеві, тобто середнє значення відхилення для будь-якої випадкової величини прямує к нулю. Тому в статистичних наукових дослідженнях для виміру варіації частіше використовують показник дисперсії.

Приклад. На основі даних таблиці 4.6.розрахуємо середнє лінійне відхилення для дискретного ряду розподілу.

Таблиця 4.6.

Розподіл вчителів середніх шкіл району за стажем роботи

Стаж роботи, років, хі	Кількість вчителів, в % до підсумку, fi	xifi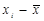
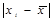
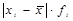
А
			-2 -1		-28 -20
Разом			-	-

Розмах варіації за стажем складає:

R=12 – 8 = 4 роки.

Допоміжні розрахунки наведені в графах 3 – 6 таблиці.

Середній стаж роботи визначимо за формулою середньозваженої арифметичної:

років.

Середнє лінійне відхилення стажу роботи вчителів середніх шкіл району складає:

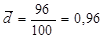роки.

Дисперсія( 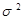- сігма-квадрат) представляє собою середній квадрат відхилень індивідуальних значень ознаки від її середньої величини. Дисперсія розраховується за формулами простої середньої незваженої і зваженої відповідно:

;

.

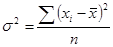На практиці застосовують більш просту формулу для розрахунку дисперсії:

.

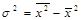Середнє квадратичне відхилення (σ) – це корінь другого ступеню із середнього квадрата відхилень певних значень ознаки від їх середньої:

(для незгрупованих даних);

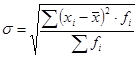(для згрупованих даних).

Приклад. Розрахуємо дисперсію і середнє квадратичне відхилення для наступного ряду розподілу (табл..4.7.)

Таблиця 4.7.

Розподіл магазинів міста за товарообігом в ІІ кварталі 1998 року

Групи магазинів за величиною товарообігу, тис. грн.,	Число магазинів, fi	Середина інтервалу, т. грн., хі	xifi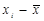
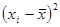
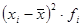
А
40-50 50-60 60-70 70-80 80-90 90-100 100-110 110-120 120-130 130-140				-49,2 -39,2 -29,2 -19,2 -9,2 0,8 10,8 20,8 30,8 40,8	2420,64 1536,64 852,64 368,64 84,64 0,64 116,64 432,64 948,64 1664,64	4841,28 6146,56 5968,48 3686,40 1269,60 12,80 2566,08 4759,04 5691,84 4993,92
Разом		-		-	-	39936,00

При розрахунку показників варіації за інтервальним рядом розподілу необхідно спочатку визначити середини інтервалів, а потім вже вести подальший розрахунок, розглядаючи ряд середин інтервалів як дискретний ряд розподілу.

Результати допоміжних розрахунків для визначення дисперсії та середнього квадратичного відхилення знаходяться в графах 2 – 6 таблиці 4.7.

Середній розмір товарообігу визначається за середньозваженою арифметичною і складає: тис. грн.

Дисперсія товарообігу .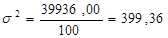

Середнє квадратичне відхилення товарообігу визначається як квадратний корінь з дисперсії: тис. грн.

Для порівняння варіації різних ознак або однієї ознаки в різних сукупностях використовують відносні показники варіації. Коефіцієнти варіації розраховуються як відношення абсолютних характеристик варіації (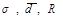) до центру розподілу і часто виражаються процентами. Отже:

1. Коефіцієнт осциляції:

2. Лінійний коефіцієнт варіації:

3. Квадратичний коефіцієнт варіації:

В статистиці сукупності, що мають коефіцієнт варіації (V_σ) більший 30-35%, вважаються неоднорідними.

Приклад. За даними вибіркових обстежень домогосподарств, середньодушові витрати на харчування становили 80 гр. од.; на придбання промислових товарів – 35; дисперсії відповідно – 256 та 196.

Порівняти ступінь варіації витрат домогосподарств на харчування та придбання промислових товарів можна за допомогою квадратичного коефіцієнта варіації:

витрати на харчування:

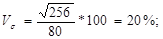
витрати на придбання промислових товарів:

Отже, ступінь варіації витрат на придбання промислових товарів значно вищий.

Дата добавления: 2013-12-14