Методи обчислення визначників n-го порядку

1)Метод приведення до трикутного вигляду шляхом елементарних перетворень

2)Метод рекурсивних перетворень

Метод рекурсивних перетворень:
Даний визначник порядку n,після перетворення і розкладання за деяким рядком,або стовпцем знову обчислюємо через визначник того ж виду,але нижчого порядку,тобто за деяке рекурсивне співвідношення обчислюють тільки визначники початкових порядків, скільки їх входить в праву частину рекурсивних співвідношень. Обчислення проводять доти, доки не знайдуть закономірність.
Приклад

Обчислити визначник.

3 2 0 0 …….. 0 0

1 3 2 0 …….. 0 0
J_n = 0 1 3 2 …….. 0 0 =

0 0 1 3 ……... 0 0

0 0 0 0 ……… 1 3

1) Розкладаємо визначник по першому рядку і першому стовпцю:

3 2 0 ….. 0 0 2 0 0 ………0 0

1 3 2 ….. 0 0 1 3 2 ………0 0

=3_*(-1)¹⁺¹ 0 1 3 ……….. +1_*(-1)¹⁺² 0 1 3 ……...0 0

…………………. …………………..

0 0 0 ….. 1 3 0 0 0 ……..1 3

2) Другий визначник порядку J_n-1 розкладемо по першму рядку:

2 0 0 ……..0 0 3 2 …. 0 0

1 3 2 ………0 0 1 3 …..0 0

0 1 3 ………0 0 ……………..

(-1)¹⁺² ………………….. = 3 J_n-1 -2 ………………

0 0 0 ……...1 3 0 0 ……1 3

Отримали співвідношення J_n=3 J_n-1-2 J_n-2

Запишемо характерестичне рівняння дляданого співвідношення, а саме візьмемов якості визначника найменшого порядку J_n-2 ->1

J_n-1->r;

J_n->r²;

Маємо рівняння:

r²=3r-2

r²-3r+2=0 – отримали квадратне рівняння. Знайдемо корені даного рівняння:

r1=2;

r2=1; 1

Корені різні – дійсні.

Правило 1 якщо розв’язок характеристичного рівняння має різні дійсні корені, то загальне рівняння має вид: r_n=C₁r₁ⁿ+C₂r₂ⁿ - (вираз 1),

де C_1,C₂ – деякі сталі коефіцієнти, а n- порядок визначника.

Отже, r_n= C_1*2ⁿ+C₂=J_n

J_n =3

3 2

J₂ = 1 3 = 9-2 =7

3 2 0

J₃ = 1 3 2 = 27+0+0-0-6-6=15

0 1 3

J₄ = 3 J₃-2 J₂ = 3_*15 – 2_*7=45-14=31

Знайдемо сталі C_1, C_2.

Для цього в вираз 1 підставимо n=1, маємо: r1= J₁= C_1*2+ C₂=3
Фіксуємо n=2, маємо: r2= J₂= C_1*2²+ C₂=7

r1= J₁= C_1*2+ C₂=3

r2= J₂= C_1*2²+ C₂=7

Отримали систему лінійних рівнянь з двома невідомими відносно C_1, C_2.

2 C₁-4 C₁+ C₂- C₂=3-7

-2 C₁=-4

C₁=2

C₂=3-4=-1

Отже, частинний розв’язок має вид: J_n =2_*2ⁿ+(-1)=2ⁿ⁺¹-1.

Правило 2 якщо при розв’язку квадратного характеристичного рівняння отримали рівні корені r1=r2=r, то загальний розв’язок має вид: r_n=(C₁+C_2*n)*rⁿ

C ₁ = ;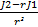

C₂=;

Дата добавления: 2013-12-14