Знайдемо рівняння

Еліпс

Криві другого порядку

Лекція 5

1. Еліпс

2. Гіпербола

3. Парабола

Загальний вид кривих другого порядку: Ах²+2Вху+Су² +Dх+С₁у+F=0 (1),

де A,B,C,D,C₁,F=const

Нехай В=0 тоді, якщо

1) А = С – рівняння є колом

2) А·С>0 - рівняння є еліпсом

3) А·С <0 - рівняння є гіперболою

4) А·С = 0 - рівняння є параболою

Означення: Еліпсом називається геометричне місце точок площини, сума відстаней від яких до двох фіксованих точок(фокусів) є величина стала й рівна 2а.

Нехай фіксовані точки (фокуси) площини F₁ і F₂. Точка М(х,у) – деяка точка площини.

За означенням відстань |F₂M|+|F₁M| = 2a = const (2)

Проведемо через точки F₁ і F₂ – пряму х, відстань F₁F₂ ділимо навпіл і проведемо ОУ, отже, |OF₂|=|OF₁|

Позначимо відстань між |F₁ F₂| = 2с – фокусна відстань, тоді координати F₁(-с,0), F₂(с,0)

F₂M = (х-с;у-0)

F₁M = (х+с; у-о)

|F₂M| =

|F₁M| =

^{Підставимо в (2):}

+= 2а

Маємо ірраціональне рівняння.

Зробимо перетворення ² =(2а-)²

(х-с)²+у²=4а²- 4а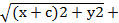(х+с)²+у²

4а=4а²+х²+2сх+с²-х²+2сх-с²

а²((х+с)²+у²)=а⁴+2сха²+с²х²

х²(а²-с²)+а²у²=а²(а²-с²)

Позначимо b²= а²-с²

b²x²+a²y² = a²b²
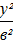+ = 1 – канонічне рівняння еліпса (3)

Відстань |F1F2| називається фокусною відстанью.

С = - називаються лінійним ексцентриситетом.

Позначимо вершини еліпса А₁, А₂ на осі ОХ, на осі ОУ В₁, В₂

|А₁А₂| - велика вісь = 2а

|В₁В₂| - мала вісь = 2b

Отже координати вершин мають вид: А₁(а,0); А₂(-а.0); В₁(0,-в); В₂(0,в); F₁(-с.0); F₂(с,0).

Для того щоб побудувати еліпс необхідно:

1) Провести прямі х = а; х = -а;

2) Провести прямі у = b; у = -b;

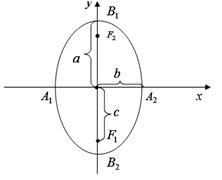В отриманий прямокутник вписати еліпс.

Зауваження: фокуси еліпса завжди заходяться на великій вісі, якщо в<а, то фокуси знаходяться на вісі ОУ. Тоді |В₁В₂| - велика вісь |А₁А₂| - мала вісь F₁(0,-c) F₂(0,c)

Означення: Ексцентриситетом еліпса називається відношення фокусної відстані 2с до довжини великої вісі.

У випадку. Коли а>в - Е = 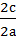, коли а<в - Е =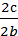

Приклад 1. Побудувати еліпси

1) + = 1 2) += 1

Розв’язання

a² = 4 -> a = ±2 |a|<|b| -> еліпс витягнуто вздовж осі ординат

b² = 9 -> b = ±3 |a|<|b| -> еліпс витягнуто вздовж осі абсцис

Знайдемо координати фокусів

1) С =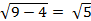

F₁(0; -√5)

F₂(0; √5)

2) F₁(√3; 0)

F₂(-√3;0)

Приклад 2. Скласти канонічне рівняння еліпса фокуси якого є вісі абсцис симетрично відносно початку координат, якщо відстань між _|F₁ F₂| = 8, Е=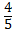

Розв’язання

2с=8; с=4.

|a|>|b|

а=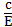= 5

b= =3

Тому рівняння еліпса має вид: + = 1

Зауваження: Ексцентриситет еліпса знаходиться в межах від 0 < E < 1 і він вказує на кривизну еліпса, тобто чим менший, тим він більше витягнутий вздовж більшої вісі.
На практиці ексцентриситет можна знайти за формулою:

Е = = , де a>b (4)

Е = . де a<b (5)

Означення. Дві прямі називаються директрисами еліпса, якщо їх рівняння має вид:

Х = ± , коли a>b

У = ± , коли a<b

Означення. Фокальними радіусами довільної точки М еліпса називаються відрізки прямих, що сполучають цю точку з фокусами F₁, F_2.

Їх довжини обчислюються за формулами:

r₁ = a – Ex

r₂ = a + Ex, коли a>b

r₁ = b – Ey

r₂ = b + Ey, коли a<b

Приклад. Знайти канонічне рівняння еліпса:

16х²+9у²+64х-54у+1 = 0 – рівняння задано в загальному вигляді.

Коефіцієнти при х² А=16

у² С=9

А·С = 144 > 0; A≠C, маємо рівняння еліпса.

Згрупуємо окремо змінні х і у.

Коефіцієнти при х², у² винесемо за дужки, маємо:

16(х²+4х)+9(у²-6у)+1=0

Виділимо повний квадрат:

16(х+2)²+9(у-3)²=144 |:144

Маємо: 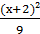+= 1

Рівняння еліпса зі зміщеним центром. Знайдемо координати центра, для цього прирывняэмо кожну душку до 0.
х+2 = 0 х = -2

у-3 = 0 у = 3

О(-2, 3)

Побудуємо еліпс.

Знайдемо координати фокуса в системі X₁O₁Y₁

F₁(0;-C) = F₁(0;-)

F₂(0;C) = F₂(0;)

Знайдемо ексцинтриситет

E =

Знайдемо рівняння фокальних радіусів

r₁ = b-Ey = 4-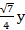

r₂ = b+Ey = 4+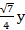

Знайдемо рівняння директриси

Y = ± => y = ±

Дата добавления: 2013-12-14