Елементи випуклого аналізу

Розподіл функцій між людиною-оператором. і технічними засобами АСК

Вивчення досвіду впровадження АСК у різноманітних сферах переконує нас у тому, що провідна роль у цих системах зали­шається за людиною-оператором. Фактично обсяг так званої рутинної роботи, якою доводиться займатись управлінському персоналові, не зменшується з впровадженням у процес керу­вання ЕОМ. Однак використання ЕОМ у керуванні корінним чином змінює форми розумової праці людини. Концепція повної автоматизації переробки інформації не витримує сьогодні випробування часом у зв'язку із завданням творчого характеру.

Звідси випливає необхідність виділити окремо завдання, що розв'язує людина-оператор, і завдання, що розв'язує ЕОМ. На основі цього вирішується питання, які завдання передаються в системі технічним засобам разом з ЕОМ, і які на відповідному етапі розвитку АСК залишаються за людиною. Особливого значення набуває тут аспект взаємодії людини і ЕОМ у розв'язуванні завдань, процес вирішення яких виявляється поді­леним між людиною і ЕОМ.

Розподіл функцій керування в АСК має базуватися, по-перше, на інженерно-психологічній оцінці та використанні вислі-дів вивчення психічних здібностей людини, по-друге, на систем­ному підході до використання ЕОМ. Таким чином, об'єктами у розподілі функцій керування на певному етапі розвитку АСК є: множина завдань, що розв'язуються в системі керування; множи­на функцій, що виконуються при розв'язуванні цих завдань; опе­ративний апарат або окремий оператор; технічні засоби АСК (ЕОМ).

Визначальний фактор у розподілі функцій — набір парамет­рів людини й ЕОМ, які характеризують якість виконання покла­дених на них функцій (табл. 5.1).

Показник	Людина	ЕОМ	Людина+ЕОМ
Здатність працюва­ти в несподіваних ситуаціях Робота з непов­ною інформацією   Вибір способу дії   Швидкість виконання обчислень   Точність виконання операцій   Надійність   Працездатність	Висока гнучкість і здатність пристосовуватися Здатна відтворити цілісну подію Великі можливості вибору Порівняно мала   Низька Низька Залежить від втоми	Практично неможливо запрограмувати всі випадковості Практично неможлива Обмежені можливості вибору Висока   Довільна Задовільна Постійна	Людина комбінує програми і методи, скориговує роботу системи Людина корегує роботу ЕОМ Людина вибирає дії, єом їх реалізує Людина координує обчислення Визначається алгоритмом Вища ніж у компонентів системи ЕОМ «підстраховує людину», допомагає їй

Динамічні завдання задачі управління запасами.

Однією з найбільш відомих сфер додатку методів динамічного програмування є така область математичної економіки, як теорія управління запасами. Її предметом є розробка і дослідження математичних моделей систем, що займають проміжне положення між джерелами (виробниками) тих або інших ресурсів і їх споживачами. При математичній формалізації процесів управління запасами дуже часто доводиться використовувати стрибкоподібні функції, що не диференціюються і кусочно-безперервні. Як правило, це обумовлюється необхідністю обліку ефектів концентрації, фіксованих витрат і плати за замовлення. У зв'язку з цим отримувані завдання насилу піддаються аналітичному рішенню класичними методами, проте можуть бути успішно вирішені за допомогою апарату динамічного програмування. Розглянемо достатньо типове завдання, що виникає в процесі планування діяльності системи постачання, — так зване динамічне завдання управління запасами.

Хай є деяка система постачання (склад, оптова база і т. п.), плануюча свою роботу на 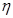періодів. Її діяльність зводиться до забезпечення попиту кінцевих споживачів на деякий продукт, для чого вона здійснює замовлення виробникові даного продукту. Попит клієнтів (кінцевих споживачів) в даній моделі розглядається як деяка інтегрована величина, що набуває заданих значень для кожного з періодів, і він повинен завжди задовольнятися (тобто не допускаються заборгованості і відмови). Також передбачається, що замовлення, що посилається виробникові, задовольняється ним повністю, і часом між замовленням і його виконанням можна нехтувати (тобто розглядається система з миттєвим виконанням замовлення). Введемо позначення:

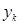— залишок запасу після (k-1) -го періоду;

— заздалегідь відомий сумарний попит в 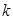-м періоді;

— замовлення (постачання від виробника) в 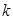-м періоді;

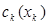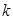— затрати на виконання замовлення об'єму в -м періоді;

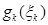— зберігання запасу об'єм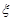у у 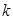-м періоді.

Після отримання постачання і задоволення попиту об'єм товару, підлягаючого зберіганню в період к, складе 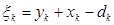. Враховуючи сенс параметра 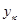, можна записати співвідношення:

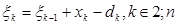(5.24)

Витрати на отримання і зберігання товару в період описуються функцією

.

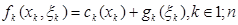За план завдання можна вважати вектор 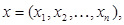компонентами якого є послідовні замовлення протягом даного проміжку часу. Співвідношення між запасами (5.24) у поєднанні з деякою початковою умовою пов'язує стани системи з вибраним планом і дозволяє виразити сумарні витрати за всі періодів функціонування| керованої системи постачання у формі|у формі| адди­тивної| цільової функції:

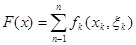(5.25)

Природним в рамках сформульованої моделі представляється завдання знаходження послідовності оптимальних управлінь (замовлень) 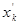і зв'язаних з ними оптимальних станів (запасів) 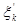, які обертають в мінімум (5.25). Як початкова умова використовуємо вимогу про збереження після завершення управління заданої кількості товару , а саме

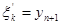(5.26)

При рішенні поставленої задачі методом динамічного програмування як функція стану керованої системи 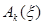логічно узяти мінімальний об'єм витрат, що виникають за перших до періодів за умови, що в 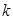-й період є запас 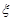. Тоді можна записати основне рекурентне співвідношення

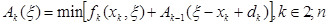(5.27)

Оскільки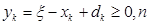

Система рекуррентних співвідношень (5.27)-(5.28) дозволяє знайти послідовність функцій стану і умовних оптимальних управлінь 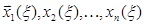На 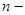м кроці за допомогою початкової умови (5.26) можна визначити 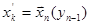. Інші значення оптимальних управлінь 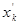визначаються за формулою:

(5.29)

Особливий інтерес представляє окремий випадок завдання (5.24) -(5.25), при якому передбачається, що функції затратна поповнення запасу 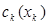є увігнутими по , а функції витрат на зберігання 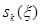є лінійними щодо об'єму запасу, що зберігається, тобто . Паралельно відмітимо, що обидві передумови є достатньо реалістичними.

Позначимо функцію витрат|затрат| протягом 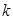-го періоду через

(5.30)

або, що те ж саме

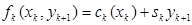(5.31)

Через зроблені припущення всі функції витрат 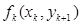є увігнутими (як суми увігнутої і лінійної функцій). Дана властивість значно спрощує процес рішення, оскільки для пошуку мінімуму увігнутих функцій 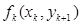досить розглянути тільки дві крайні точки множини, на якій відшукується мінімум. З урахуванням введеного позначення завдання (5.24)~(5.25) можна записати у вигляді:

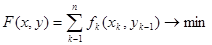(5.32)

при умовах

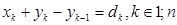(5.33)

Розглянемо процедуру вирішення (5.32)-(5.33). Так як знаходиться мінімум суми ввігнутих функцій f_k(x_k, y_k+l), то відповідь буде досягатися на одній із крайніх точок множини, що визначається умовами (5.33). загальне число змінних x_k та у_к в системі (5.33) рівно 2. Однак, враховуючи те, що в ній тільки рівнянь в оптимальному плані буде не більше ненульових компонент, причому для кожного періода k значення х_к та yk не можуть рівнятися нулю одночасно (в силу необхідності задоволення попиту або за рахунок замовлення, або за рахунок запа­су|). Формально це твердження|затвердження| можна представити|уявляти| у вигляді умови| доповнюючої нежорсткості:

(5.34)

де

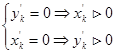(5.35)

З погляду змістовної інтерпретації умови (5.34) -(5.35) означають, що при оптимальному управлінні замовлення постачальникові на нову партію не повинне поступати, якщо на початку періоду є ненульовий запас, або розмір замовлення повинен дорівнювати величині попиту за ціле число періодів. Звідси витікає, що запас на кінець останнього періоду повинен дорівнювати нулю: . Останнє дозволяє вирішувати задачу в прямому напрямі, застосовуючи рекурентне співвідношення

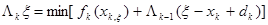(5.36)

Враховуючи (5.34) -(5.35) і угнутість 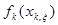укладаємо, що мінімум (5.36) досягається в одній з крайніх точок 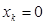або , тому

(5.37)

тоді для попереднього періоду функція стану|достатку| може бути виражена|виказувати| як

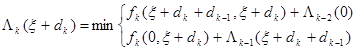(5.38)

на основі чого в загальному|спільному| вигляді|виді| отримуємо|одержуємо| модифіковану фор­му| для рекуррентного співвідношення

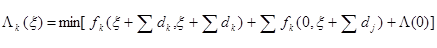(5.39)

При подальших конкретизуючих припущеннях про вид функцій fk(xk, yk+l) можна отримати ще компактніші форми для рекурентних співвідношень. Проте ці питання носять достатньо приватний характер, і ми їх розглядати не будемо. Відзначимо лише, що приведені в даному пункті перетворення непогано ілюструють загальні підходи, вживані в динамічному програмуванні, а також ті властивості завдань, які відкривають можливості для ефективного і плідного використання відповідних методів.

Якщо в деяких випадках класичні методи не дають результатів, то застосовуються чисельні методи, які являють собою обчислювальні процедури, поступово "поліпшуючі" значення цільової функції. Найбільш ефективні чисельні методи розроблені для завдань випуклого програмування (ЗВП), перевагою яких є те, що завжди мінімум (максимум) цільової функції існує і є абсолютним (глобальним). Ця властивість гарантує збіжність чисельних методів до правильного рішення.

Загальна постановка задачі випуклого програмування (ЗВП) має вигляд:

знайти: 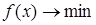, 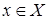(1)

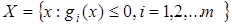при (2)

де f(x), g_і(x) — випуклі функції.

Функція f(x), визначена на деякій множині X, називається випуклою, якщо для будь-яких точок x₁ і х₂ з X і довільного числа λ: 0 < λ 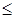1 виконується .

Зокрема, для функції одна змінної ця нерівність означає, що відрізок, що з'єднує довільну пару точок її графіка, ні в яких інших точках цей графік не перетинає.

Наприклад, функція f(x)=x² є випуклою на всій числовій осі, а функція f(x)=sіn(x) випукла на проміжку [π,2 π].

Якщо функція f(x) — випукла, то обернена до неї -f(x) — увігнута.

Множина X називається випуклою, якщо для будь-яких її точок х₁ і х₂ і довільного числа k: 0 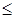k <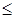1 точка у=kх₁ + (1-k) х₂ також належать цій множині. Оскільки при будь-яких значеннях k у пробігає всі точки відрізка, що з'єднує точки х₁ і х₂, то випуклою буде та множина, у якого будь-які дві крапки можна з'єднати відрізком, що повністю належить цій множині.

Якщо функція g(х) — випукла, то множина W, задана нерівністю g(х) 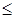0, є випуклою.

Перетин випуклих множин, заданий системою обмежень виду W={x: g_i(х) 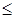0, i=1,2,...,m), де всі функції g,(х) — випуклі, є випуклою множиною.

Чисельні методи рішення ЗВП дозволяють із будь-якої точки припустимої області наблизитися до шуканого рішення. Оскільки на кожній ітерації проводяться однотипні дії, то застосування ЕОМ є особливо ефективним.

Якщо ЗВП не має обмежень, тобто відсутні умови (2), то пошук экстремума функції f(x) ведеться на всьому просторі Rⁿ (нагадаємо, що при n=1 R — це числова вісь, при n=2 — це площина i т.д.).

Вдало вибираючи напрямок руху, можна з достатньою точністю прийти до екстремальної точки за скінченне число кроків (ітерацій). Зокрема, для диференційованої функції градієнт вказує напрямок найбільшого зростання функції, а антиградієнт — напрямок спадання функції. Якщо цільова функція f(x) має й другі похідні, то напрямок руху можна уточнити за допомогою матриці Гессе. Для недиференційовних функцій перспективні напрямки вибираються серед напрямків координатних осей або напрямків, отриманих випадковим чином.

Наявність обмежень істотно ускладнює методи рішення ЗНЛП. Для того, щоб обчислювальні процедури не виводили за межі допустимої області, потрібне рішення допоміжних завдань. Наприклад, якщо напрямок градієнта (антиградієнта) є неприпустимим (виходить за межі припустимої області), то потрібна операція проектування градієнта на припустиму область, а це досить складне завдання особливо при нелінійних обмеженнях (метод проекції градієнта).

Якщо пошук ведеться в деяких можливих напрямках, що не виходять за межі області, то для вибору найкращих серед них, потрібне рішення допоміжної задачі лінійного програмування (метод можливих напрямків - Зойтендейка).

Ідея методів штрафних і бар'єрних функцій полягає у відомості ЗНЛП із обмеженнями до ЗНЛП без обмежень, оскільки останні вирішуються порівняно просто. При цьому обмеження вихідної задачі спеціальним чином включаються до складу цільової функції нової задачі (задачі без обмежень).

Дата добавления: 2013-12-14