Приклади задач динамічного прорамування

5.2.1. задача про наймання працівників. Допустимо до розглядання питаня застосування методів динамічного програмування в конкретних економічно-математичних моделях.

Розглянемо перший випадок. Оскільки фіксованим являється початкова кількість робітників і, проти, нічого невідомо про те, якою ця кількість повинна бути на останньому етапі, то розглядання процесу прийняття рішення зручно починати з кінця. Оптимальне управління на останньому етапі по умові дорівнює , тому мінімальні витримки повністю визначаються кількістю робітників в останньому періоді:

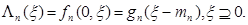(5.16)

Для інших наступних кроків основне рекурентне співвідношення має вигляд:

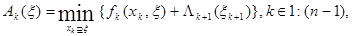(5.17)

Де - мінімальні затрати з го по 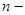й періоди, в допущенні, що кількість робітників в й період дорівнює 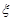. Точки , в яких досягаються мінімуми (5.17), визначають умовне оптимальне управління на кожному кроці.

Послідовно визначаючи і дійшовши до етапу 1 ми зможемо знайти безумовне оптимальне управління із тої умови, що на початок першого періода чисельність робітників повинна становити 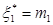, а саме:

.

Інші компоненти оптимального плану і стану , утворюючі оптимальну траєкторію, послідовно знаходяться по рекурентним формулам:

,

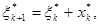
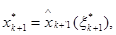
Після чого не виникає складності визначити оптимальне значення цільової функції (5.15).

Зупинимося тепер на другому випадку, коли заданий фінальний стан управляемого об´єкту, тобто бажана кількість робітників на осанньому етапі . Очевидно, що в даній ситуації треба поступити з точністю «до навпаки» і розглянути процес прийняття рішення від початку до кінця. Найкраще умовне управління на першому кроці буде знайдене в процесі знаходження функцій:

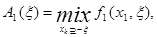
(5.18)

Де стан є можливою кількістю робітників на початковому кроці. відповідно, основне рекурентне співвідношення виразить мінімальні витримки аж до го періоду через такі для попередніх періодів (з першого по (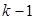)-й при умові, що чисельність робітників в й період буде дорівнювати :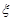

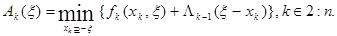
(5.19)

Попуньо будуть знайдені функції , , 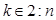визначаючі умовні оптимальні управління. На останньому періоді, в силу початкової умови, . Звідси шляхом послідовного рішення ркекурентних рівнянь можуть бути знайдені оптимальні чисельності робітників 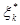у безумовні оптимальні рівняння:

.

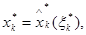
В останньому так як і в першому випадку, підраховується мінімальна величина витримок.

Узагальнюючи складені схеми рішення, можна прийти до висновку:

При дослідженні алгоритмів динамічного програмування, якщо заданий початковий стан упарвляємої системи, то задача вирішується в зворотньому напрямку, а якщо кінцеве, то -в прямому. На кінець, якщо задані як початкові, так і кінцеві стани, то задача суттєво ускладнюється. (в якості компромісу в тому випадку можна відмовитися від оптимізації на першому чи останньому етапі).

Дата добавления: 2013-12-14