Сіткові графіки

Сіткові графіки являють собою математичний апарат для представлення, вивчення і керування складними комплексами взаємозалежних робіт, спрямованих до досягнення щодо невеликого числа чітко визначених цілей.

Найбільш простими є одноцільові сіткові графіки, з яких ми і почнемо наш розгляд. Метою тут може бути закінчення будівництва того чи іншого об'єкта, створення унікального виробу, виконання науково-дослідної чи дослідно-конструкторської роботи, завершення чи реконструкції ремонту і т.п.

Найпростіший приклад одне-цільового сіткового графіка зображений на мал.. Сітковий графік складається з об'єктів двох видів: вузлів (позначених кружками) і з'єднуючих їх (спрямованих) ребер (позначених стрілками).

Кожному вузлу відповідає деяка подія, що полягає в закінченні того чи іншого етапу робіт, наприклад, «закладка фундаменту кінчена», «технічний проект прийнятий комісією» і т.д. Кожній стрілці (ребру графіка) відповідає та чи інша робота, що розуміється як процес, а не як результат, наприклад, процес спорудження стін, процес оформлення ескізного проекту і т.д. Для кожної роботи задається її тривалість, вимірювана у фіксованих для даного графіка одиницях (годинник, дні, чи тижні місяці).

Зміст графіка складається насамперед у тім, щоб указати всі технологічні зв'язки, що визначають можливі послідовності робіт. З мал. видно, що робота 6 може бути почата лише після закінчення роботи 1, а робота 7 – лише після закінчення робіт 3 і 4. У ряді випадків для завдання зв'язків приходиться користатися так називаними фіктивними роботами, що мають нульову тривалість і позначено на графіку пунктирними стрільцями.

Роль фіктивних робіт легко усвідомити з мал. 16. Робота 7 може виконуватися після закінчення робіт 3 і 4, а роботи 5 і 9 – після закінчення робіт 2, 3 і 4. Якби ми об'єднали вузли ІІІ і IV, то роботі 7 довелося б чекати закінчення не тільки робіт 3 і 4, але і роботи 2. При наявності фіктивної роботи необхідність такого чекання виключається.

На будь-якому одноцільовому сітковому графіку виділяються дві події – початкове і кінцеве. Початкова подія (у нашому випадку подія) характеризується тим, що в нього не входить жодна стрілка, а кінцеве (у даному випадку подія VI) тим, що з нього не виходить жодна стрілка. Всі інші події звуться проміжних. Початкова подія відповідає початку робіт (нульовий момент часу), а кінцева завершенню всіх робіт (досягненню поставленої мети).

Першою задачею, що виникає при аналізі сіткових графіків, є визначення часу настання кожної події і можливостей варіювання часу початку і закінчення кожної роботи. Алгоритм рішення цієї задачі дуже простий.

Припустимо, що для графіка, зображеного на мал., тривалості робіт задані наступними числами: t₁ = 3; t₂ = 7; t₃ = 5; t₄ = 3; t₅ = 5; t₆ = 6; t₇ = 3; t₈ = 2; t₉ = 6. Події І відповідає момент часу Т₁ = 0.

Щоб знайти мінімальний термін Т_і настання будь-якої іншої події (і > 2), необхідно, мабуть, прорахувати сумарні витрати часу по всіх шляхах, що веде у відповідний цій події вузол з початкового вузла, і вибрати з них максимальне значення. Усякий раз, коли для якоїсь події термін його настання встановлений, можна будувати подальші шляхи, відправляючись від цієї події, як від початкового. Для події ІІ, до якого веде тільки один шлях (робота І), одержимо

.

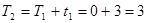Для події ІІІ маємо два шляхи. З огляду на лише роботу 3, одержимо перше (не остаточне) значення для часу Т₃, настання цієї події:

.

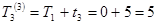Відповідне обчислення по робот 4 приводить до значення:

.

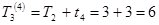Найбільше з цих двох значень і дає саме шуканий термін настання події ІІІ: Т₃ = 6.

Для події IV

; .

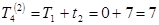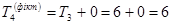Звідси Т₄ = 7. Для події V

; ; .

Таким чином, Т₅ = 12. Нарешті,

; .

Звідки Т₆ = 14.

Одержавши мінімальний термін Т₆ настання кінцевої події (а виходить, і час закінчення всіх робіт), ми можемо, відправляючись від нього і виконуючи описану процедуру в зворотному порядку, обчислити максимальні можливі терміни настання всіх подій графіка, виходячи з необхідності закінчити всі роботи в обчислений термін. Для кінцевої події думаємо 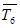= Т₆ =14. Для події V маємо = Т₆ – t₈ = 14 – 2 = 12. Для події IV маємо дві можливості (рухаючи від подій V і VI у напрямку, зворотному стрілкам):

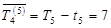; і .

З отриманих чисел необхідно, мабуть, вибрати мінімальне тобто 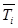= 7. Для події ІІІ одержуємо:

; .

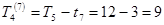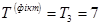Таким чином, Т₃ = 7. Для події ІІ:

; .

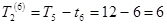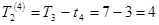Звідки Т₂ = 4.

При правильному обчисленні час настання початкової події завжди повинний бути дорівнює 0. Перевіряємо:

; ; .

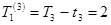Мінімальне значення дорівнює 0. Таким чином, Т₁ = 0, що підтверджує (хоча і не з абсолютною гарантією) правильність проведених нами обчислень.

Зведемо отримані значення в табл. 6.

Терміни	Події
І	ІІ	ІІІ	ІV	V	VI
Ті
Ті

З цієї таблиці видно, що для подій ІІ і ІІІ припустиме запізнення на одиницю часу без зміни загального терміну виконання робіт. Для подій /, IV, V, VI ніякі запізнення неприпустимі; будь-яка затримка в їхньому настанні спричиняє збільшення загального терміну всіх робіт. Про події, що володіють такою властивістю, прийнято говорити, що вони знаходяться на критичному шляху.

Для перебування критичного шляху для кожної j -і роботи обчислимо мінімально і максимально можливі терміни початку і закінчення роботи:

;

;

;

,

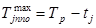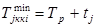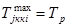де р — подія, що коштує на початку роботи j; q – у її кінці. Результати розрахунків зводимо в табл. 7.

Різниця будемо називати резервом часу для j -і роботи. Роботи, у яких резерв часу дорівнює нулю, складають критичний шлях. У нашому випадку критичний шлях складають роботи 2, 5 і 8. Інші роботи мають менші чи великі ненульові резерви часу. Зрозуміло, при використанні сіткового графіка як інструмент керування (а не тільки як засіб для початкового аналізу), необхідно здійснювати регулярне відновлення інформації (як про очікувану тривалість робіт, так і про фактичний їхній стан) і щораз

Термін	Види робіт
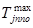
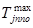
tj

заново обчислювати всі перераховані вище показники. При цьому може мінятися не тільки очікуваний час настання тих чи інших подій (у тому числі і кінцевого), але і критичний шлях. Основна перевага керування на основі мережного (а не звичайного) графіка полягає в тому, що увага керівництва може зосереджуватися на тих роботах, що є вирішальними з погляду термінів закінчення всіх робіт.

На етапі попереднього планування визначення критичного шляху супроводжується аналізом можливостей скорочення тривалості робіт, що знаходяться на цьому шляху. Облік цих можливостей з відповідним перерахуванням усього графіка визначає новий критичний шлях, для якого знову шукаються можливості скорочення термінів і так далі, поки не будуть вичерпані всі можливості подальшого поліпшення графіка. Ця робота повинна продовжуватися постійно й у процесі фактичного виконання робіт, оскільки тут можуть відкриватися нові можливості поліпшення графіка, недоступні на етапі попереднього планування, або можуть виникати нові задачі по поліпшенню графіка в зв'язку зі змінами критичного шляху.

При переході від одне-цільових сіткових графіків до багатоцільових описана вище методика тимчасового аналізу власне кажучи не міняється. Різниця складається лише в тім, що максимально можливі терміни Т_і настання подій повинні обчислюватися для кожної з поставлених цілей. Самий пізній з цих термінів визначає час рішення задачі, Т. е. досягнення всіх кінцевих цілей.

Розглянемо двох цільовий сітковий графік, зображений на мал. 17, для якого тривалості робіт задані табл. 8,

Види робіт
Термін (tj)

Діючи точно в такий же спосіб, як і в попередньому прикладі, визначимо мінімальні терміни настання всіх подій (табл. 9).

Для визначення максимально можливих термінів T_j настання подій, думаємо

T₇ = T₇ = 12 і T₈ = T₈ = 14

Позначимо через 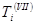і максимально можливі терміни настання події м з погляду задач досягнення окремо узятих цілей VII і VIII відповідно.

Дата добавления: 2013-12-14