Таблиця 9

Подія	I	II	III	IV	V	VI	VII	VIII
Термін (Ti)

Таблиця 10

Подія	I	II	III	IV	V	VI	VII	VIII
Термін (Ti)

Тоді , оскільки досягнення мети VII не вимагає настання події VI. З іншого боку, .

Максимально можливий термін настання події VI з погляду досягнення обох цілей:

.

Для події V одержуємо:

; .

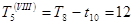Тоді . Продовжуючи таким чином, знаходимо терміни Т_і для всіх подій (таблиця 10).

Для обчислення мінімально і максимально можливих термінів початку і закінчення робіт, можна користатися тими ж формулами, що і раніш, якщо мова йде про досягнення обох цілей. Заміняючи у формулах Т_i на 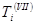і , знаходимо відповідні терміни з погляду задач досягнення кожної з цілей VII і VIII

окремо:

Наприклад,

; ; ; .

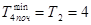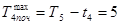Відповідно

; ;

, .

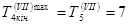Аналогічним образом обчислюємо терміни для всіх інших робіт.

Дотепер при розгляді сіткових графіків ми мали справу лише з проблемами, що стосуються лише термінів виконання і тривалості робіт. Набагато більш важкими є проблеми, зв'язані з розподілом ресурсів при плануванні і керуванні на основі сіткових графіків. Такі проблеми зводяться до задач нелінійного цілочисельного програмування дуже великого обсягу, рішення яких представляє великих труднощів навіть при використанні самих могутніх ЕОМ. На практиці тому обмежуються спрощеними постановками задачі і частковою оптимізацією, без гарантії досягнення абсолютного оптимуму.

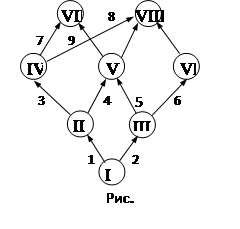
Для кращого з'ясування сутності проблем, що встають у зв'язку з оптимізацією розподілу ресурсів при плануванні і керуванні на основі сіткових графіків, розглянемо наступний приклад. Нехай сукупність підлягаючих виконанню робіт описується сітковим графіком, зображеним на мал. Припустимо, що мається всього два ресурси R₁ і R₂, що підлягають розподілу (робітники двох чи спеціальностей устаткування двох різних видів).

Таблиця 11

Ресурси

Види робіт

4

å

R1

R2

На всьому протязі робіт оперуємо двома одиницями першого ресурсу (наприклад, двома бригадами робітників) і трьома одиницями другого ресурсу. Припустимо, що час робіт обчислюється місяцями, а витрати ресурсів (у ресурсо-місяцях) для робіт 1, 2 ,..., 12 приведені в табл. 11. В останньому стовпці зазначені сумарні витрати, необхідні для виконання всіх робіт. Поділяючи ці витрати на наявні в наявності ресурси, одержимо мінімальний час для виконання всіх робіт:

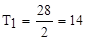міс; міс.

Критичним ресурсом (що обмежує знизу термін виконання робіт) у даному випадку буде ресурс R₁.

Мінімально можливе час виконання всіх робіт Т ³ 14мес. Цей час являє собою теоретичну межу (не завжди досяжний) для оптимізації плану виконання робіт.

Складаємо початковий. план, при якому дотримується технологічна послідовність виконання робіт, задана розглянутим сітковим графіком. У нашому випадку як такий план може бути, наприклад, прийняте послідовне виконання всіх робіт у порядку росту їхніх номерів. При цьому щораз усі наявні ресурси цілком кидаються на виконання однієї роботи і лише після її закінчення перекидаються на наступну.

Для першої роботи як по першому, так і по другому ресурсі час t_i її виконання однаково до дорівнює одному місяцю. Втрат (простоїв) ресурсів при цьому немає. При виконанні другої роботи критичним є перший ресурс. Обчислений по ньому час виконання роботи t₂ дорівнює міс. При роботі протягом цього терміну розташовуємо 3 ´ 2 = 6 ресурсо-місяцями по другому ресурсі. Оскільки фактично для виконання другої роботи потрібно лише 3 ресурсо-місяця, то по ресурсі R₁ утвориться втрата, рівна 6 – 3 = 3 ресурсо-місяцям. Продовжуючи аналогічним образом, зведемо час, а також сумарні витрати і втрати ресурсів при обраному порядку виконання робіт наростаючим підсумком (тобто у виді сум по усім виконаним до розглянутого моменту роботам) у табл. 12.

Таблиця 12

	Види робіт
Показники	1	2	3	4	5	6		8	9	10	11	12
Затрати: R1
R2
Втрати: R1
R2
Час

Очевидний недолік побудованого плану полягає в тому, що відбуваються втрати критичного (першого) ресурсу. Саме в результаті цих втрат отриманий термін виконання робіт (17 міс.) на 3 мес. більше, ніж теоретично припустима межа.

Припустимо, що ресурси R₁ і R₂ допускають незалежне використання і при виконанні будь-якої роботи можуть витрачатися в будь-якому порядку. Основна ідея по поліпшенню початкового плану при такім припущенні полягає в тому, щоб починати використання ресурсу, що звільнився, для виконання наступних робіт, не чекаючи повного вивільнення всіх ресурсів.

Взаємозалежні ресурси, наприклад муляри і піднімальні механізми, звичайно поєднуються в єдині» комплексний ресурс. Якщо робота допускає використання ресурсів тільки в одному порядку, то неї варто звести до декількох робіт, увівши нові події на вихідному сітковому графіку.

Очевидно, що така тактика приведе до успіху лише в тому випадку, коли робота, у якій починається використання ресурсу, що звільнився, є критичної у відношенні саме цього ресурсу. Це досягається зміною порядку виконання робіт, зрозуміло, при строгому дотриманні умов черговості робіт, що випливають з вихідного сіткового графіка.

Для полегшення вибору належної черговості виконання робіт розділимо їх на три групи: критичні по першому, другому і по обох ресурсах. У першу групу попадають роботи 2, 3, 6, у другу – роботи 5, 9, 10 і в третини-роботи 1, 4, 7, 8, 11, 12. Роботи останньої групи можуть виконуватися в будь-який час, що допускається вихідним сітковим графіком, не створюючи небажаних утрат ресурсів. Проблема складається у визначенні правильної

послідовності робіт першої і другої групи.

Оскільки при виконанні другої роботи утвориться резерв 3 ресурсо – місяця по ресурсі R₂, то бажано, не чекаючи закінчення цієї роботи, почати критичну по R₂ роботу, у якій цей ресурс бажано цілком використовувати. Такий є, мабуть, робота 5.

Для роботи 3 такими можуть бути роботи 5, 9 і 10, а для роботи 6–9 і 10. Одним з можливих рішень, що дають необхідну черговість, служить послідовність виконання робіт 1, 2, 5, 4, 7, 6, 9, 3, 10, 8, 11, 12, для якої всі показники приведені у табл. 13.

Показники

Види робіт

Час початку використання ресурсу R1

Час заверш. використання ресурсу R1

Час початку використання ресурсу R2

Час заверш. використання ресурсу R2

Час початку роботи

Час завершення роботи

Використання R1 R2

Втрати R1 R2

У розглянутому випадку удалося досягти теоретичної межі для часу виконання робіт і цілком уникнути втрат критичного ресурсу. Неважко зрозуміти, що, оскільки мова йде про перебування належної перестановки вихідного порядку виконання робіт, то, замість застосованого прийому угадування потрібного порядку, можна застосувати загальний метод динамічного програмування, аналогічно тому, що був застосований у задачі про комівояжера. Відмінність складається лише в тім, що розгляду підлягають не всі можливі підстановки, а тільки.ті з них, у яких послідовність робіт задовольняє вимогам вихідного сіткового графіка.

У загальному випадку при оптимізації використання ресурсів приходиться розглядати можливості рівнобіжного виконання робіт, що ще більш ускладнює задачу.

Дата добавления: 2013-12-14